7. Системы, основанные на скользящих средних.
7.1. Использование скользящих средних в МТС.
7.1.1. Что такое скользящее среднее?
Идея скользящих средних наиболее естественным образом вводится на основе понятия о временных рядах, т.е. последовательности данных, расположенных в хронологическом порядке. Примером таких данных являются ежедневные цены закрытия каких-либо финансовых инструментов. Они образуют последовательность точек данных, следующих друг за другом во времени.
Во временном ряду выборка из нескольких последовательных точек данных может быть названа «временным окном». Если сумму точек например, цены закрытия) в данном временном окне разделить на количество точек этих данных, то получится среднее.
Скользящее среднее получается тогда, когда этот процесс повторяется снова и снова при смещении временного окна вперед, точка за точкой, по ряду данных. Средние величины, полученные таким образом, образуют новый временной ряд, новый набор упорядоченных во времени значений. Эта новая серия данных называется скользящей средней исходного временного ряда (в данном случае скользящее среднее цен закрытия). Этот вид скользящих средних известен, как простое скользящее среднее, поскольку рассчитывается как простое арифметическое среднее точек данных.
Скользящие средние используются для снижения нежелательного шума во временных рядах, чтобы поведение рынка, лежащее в основе процесса ценообразования, стало более понятным и заметным, яснее выраженным.
Скользящее среднее обеспечивает сглаживание данных. Как метод сглаживания скользящее среднее является специфическим фильтром нижних частот, пропуская низкочастотную активность и подавляя высокочастотные быстропеременные процессы. На графике цен высокочастотные процессы выглядят как быстрые вертикальные колебания, т.е. как шум, а низкочастотные – как более плавные тренды или волны.
Помимо способности снижать зашумленность временных рядов скользящие средние обладают преимуществами простоты, наглядности и функциональности. Однако при этом, как и любой мощный метод фильтрации или сглаживания данных в реальном времени, они имеют недостаток – запаздывание. Хотя сглаженные данные чище и, следовательно, более подходят для анализа, возникает запаздывание между данными в исходной серии и в сглаженной последовательности данных. Такое запаздывание может представлять серьезную проблему при необходимости быстрой реакции на события, как это бывает важно для трейдеров.
В некоторых случаях запаздывание не проблема, например, в системах, где линия цен пересекает скользящее среднее – фактически цена и должна обгонять среднее, чтобы такая система работала. Запаздывание более проблематично в моделях, где для принятия решений используются точки разворота графика скользящего среднего или его наклон. В таких случаях запаздывание означает отсроченный отклик, что, скорее всего, приведет к невыгодным сделкам.
7.1.3. Виды скользящих средних.
Все скользящие средние сглаживают временные ряды с помощью некоторого усредняющего процесса. Отличия состоят только в том, какой удельный вес присваивается каждой из точек суммирования и насколько хорошо адаптируется формула к изменению условий. Различия между видами скользящих средних объясняются разными подходами к проблеме снижения запаздывания и увеличения чувствительности. Более подробно этот вопрос рассмотрен в соответствующем разделе «Краткого курса начинающего трейдера».
Модели МТС, основанных на скользящих средних, генерируют сигналы на покупку или продажу на основе соотношений между скользящим средним и ценой или между двумя (или более) скользящими средними.
Существуют модели и трендследящие и контр-трендовые.
Наиболее популярные модели следуют за трендом и отстают от рынка. С другой стороны, модели, идущие против тренда, предсказывают развороты. Это не означает, что следующие за рынком модели работают хуже противотрендовых; надежные входы в тренд, пусть даже и с запаздыванием, лучше и, в общем выгоднее, чем попытки предсказывать развороты, которые только изредка происходят в ожидаемый момент – глобальный экстремум обычно бывает один, в то время как локальных будет множество.
Трендследящие методы генерации входных приказов (торговых сигналов) на основе скользящих средних могут осуществляться различными способами.
Одна из простых моделей основана на пересечении скользящих средних: трейдер покупает, когда цены поднимаются выше скользящего среднего, и продает, когда цены опускаются ниже его.
Вместо ожидания пересечения линии среднего и цен можно использовать быстрое среднее и его пересечение с более медленным. Сигнал на покупку возникает, когда быстрое среднее поднимается выше медленного, сигнал на продажу – когда быстрое среднее опускается ниже медленного. Сглаживание исходных рядов данных за счет использования скользящих средних снижает количество ложных пересечений и, следовательно, уменьшает частоту убыточных сигналов.
Еще один способ применения скользящих средних основан на использовании пересечения скользящего среднего и смещенного вперед скользящего среднего с теми же параметрами. В этом случае сигнал на покупку возникает, когда быстрое исходное среднее поднимается выше смещенного, сигнал на продажу – когда исходное среднее опускается ниже смещенного. Выбором величины сдвигах можно уменьшить количество ложных пересечений, уменьшая частоту убыточных сигналов.
Иногда используют одновременно несколько сдвинутых скользящих средних с различным сдвигом и разными периодами, как например, в аллигаторе Б.Вильямса.
Скользящие средние могут также использоваться для получения сигналов входа в противотрендовых системах. Цены часто реагируют на линию скользящего среднего примерно так, как на уровни поддержки и сопротивления, на чем и основывается правило входа, согласно которому покупают, когда цены опускаются до скользящего среднего или пересекают его сверху вниз, и продают, когда они поднимаются до нее или пересекают снизу вверх. Предполагается, что цены отскакивают от уровня скользящего среднего, изменяя направление движения.
При изучении материалов раздела и анализе параметров МТС раздела нам понадобится ряд пользовательских индикаторов. Построим их заблаговременно.
7.3.1. Скользящая средняя по цене закрытия.
N1:=Input(“Период”, 3,300,21);
Mov(C,N1,E);
7.3.2. Скользящая среднеяя по медианной (средней) цене.
N1:=Input(“Период”, 3,300,21);
Mov((H+L)/2,N1,E);
7.3.3. Скользящая средняя со сдвигом
Для цены закрытия:
N1:=Input(“Период”, 3,100,21);
N2:=Input(“Сдвиг”, 0,30,5);
Mov(ref(C,-N2),N1,E);
Для медианной цены:
N1:=Input(“N1”, 3,100,21);
N2:=Input(“N2”, 0,30,5);
Mov(ref((H+L)/2,-N2),N1,E);
7.3.4. Аллигатор Б.Вильямса.
Популярный, особенно среди новичков, индикатор в версии для экспоненциальных скользящих средних:
Mov(Ref((H+L)/2,-8),25,E); {аллигатор – синяя линия}
Mov(Ref((H+L)/2,-5),15,E); {аллигатор – красная линия}
Mov(Ref((H+L)/2,-3),9,E); {аллигатор – зеленая линия}
7.4.1. Торговая идея.
Простейшая торговая стратегия, основанная на использовании скользящих средних, основана на использовании пересечения цены и скользящей средней.
В основу этой стратегии положена простая торговая идея: скользящая средняя на трендовом рынке отстает от цены (вследствие самого принципа расчета скользящей средней). Поэтому считается, что если цена больше своей скользящей средней, то тренд восходящий, а если цена меньше скользящей средней, то тренд нисходящий.
Соответственно, если цена пересекает свою скользящую среднюю, то можно считать, что направление тренда изменилось (см.рис. 7.1.).
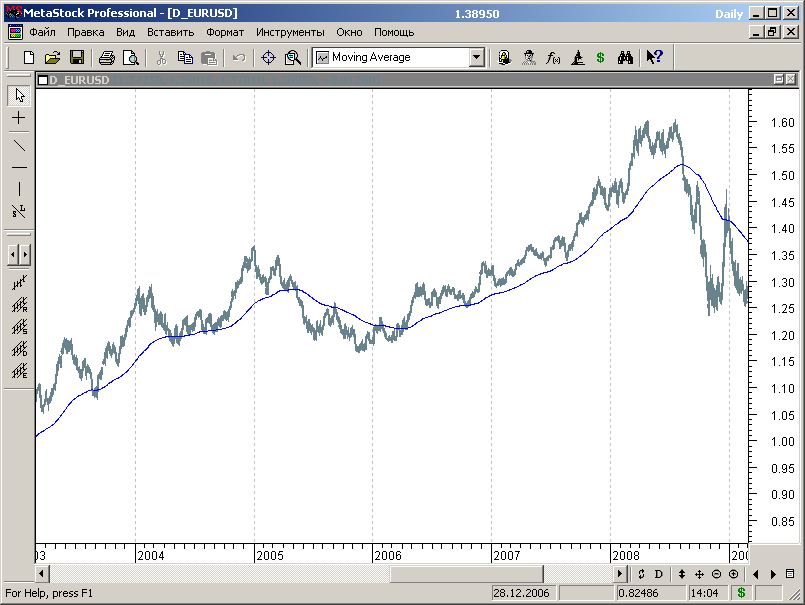
Рис.7.1.
Использование этого простейшего принципа и положено в основу простейшей МТС на основе скользящей средней.
Визуально, глядя на график, можно предположить, что этот подход к торговле потенциально способен принести нам прибыль. Проверим это тестированием.
Скользящая средняя имеет один изменяемый параметр – период.
Поэтому торговые правила для оптимизируемой торговой стратегии на основе пересечения цены и экспоненциальной скользящей средней будут иметь вид:
Buy Order: Cross(C,Mov(C,opt1,E))
Sell Order: Cross(Mov(C,opt1,E),C)
Sell Short Order: Cross(Mov(C,opt1,E),C)
Buy to Cover Order: Cross(C,Mov(C,opt1,E))
Для фиксации момента пересечения мы использовали уже знакомую нам по предыдущим разделам функцию Cross.
Открываем тестер систем, и строим новую торговую систему с вышеуказанными торговыми правилами.
Для первоначальной оптимизации в пределах стартового сегмента диапазон переменной оптимизации зададим от 5 до 300 с шагом 5.
теперь можно приступать к тестированию и оптимизации системы.
Напоминаем разбиение исторических данных по сегментам:
- основной (стартовый) сегмент – с 01.01 1990 по 31.12 1998;
- 1-й дополнительный сегмент – с 01.01.1999 по 31.12.2001;
- 2-й дополнительный сегмент – с 01.01.2002 по 31.12.2004;
- 3-й дополнительный сегмент – с 01.01.2005 по 31.12.2007;
- 4-й дополнительный сегмент – с 01.01.2008 по 31.12.2010.
Загружаем стартовый сегмент и проводим первоначальную оптимизацию.
Диаграмма результатов тестирования, упорядоченная по росту периода скользящей средней, представлена на рис.7.2.
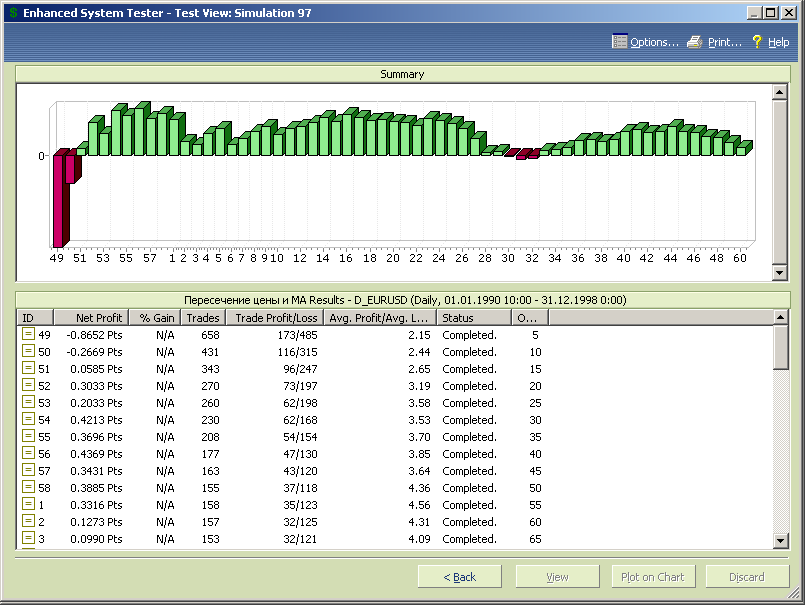
Рис.7.2.
Представленные результаты показывают следующее:
- стратегия является прибыльной при большинстве значений параметра оптимизации, т.е. модель работоспособна, а прибыль не является результатом случайного стечения обстоятельств, а результатом учета в модели свойств рынка;
- стратегия в заданном диапазоне переменной оптимизации имеет три оптимума, расположенные в окрестности значений opt1 равных 40, 130 и 270 (два последних значения указывают на существование на рынке цикла с периодом кратным или дробно-кратным значениям оптимумов).
Количество сделок с ростом периода скользящей средней убывает, но даже для opt1=270 остается достаточно большим (56), чтобы доверять результатам теста.
Выбор диапазона параметров для дальнейшей оптимизации МТС проведем на основании сравнительного анализа кривых эквити в точках оптимума.
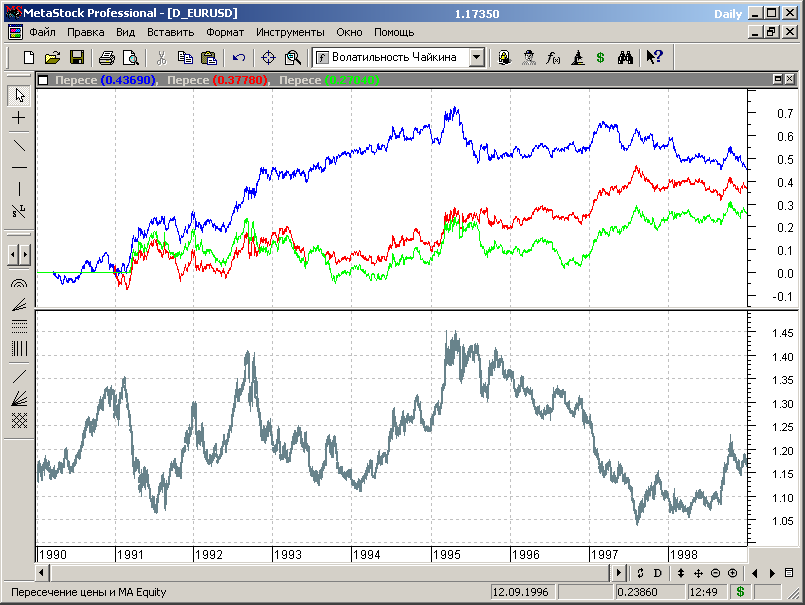
Рис.7.3.
Синим цветом показана кривая эквити для периода МА 40, красным - для 130 и зеленым – для 270.
В общем, выбирать особо не из чего. Прибыльность для параметра 40 лучше, но вторую половину диапазона тестирования стратегия не приносила прибыли.
В принципе, если брать весь диапазон в целом, то наилучшие перспективы с точки зрения плавности хода линии эквити имеет МТС с значением параметра 130, хотя это тоже не тот результат, за который следует бороться. Протестировать стратегию на всем диапазоне данных, а также проверить ее эффективность с помощью процедуры циклической оптимизации можно самостоятельно, а мы пойдем дальше, рассматривая другие методы построения торговых стратегий на основе скользящих средних.
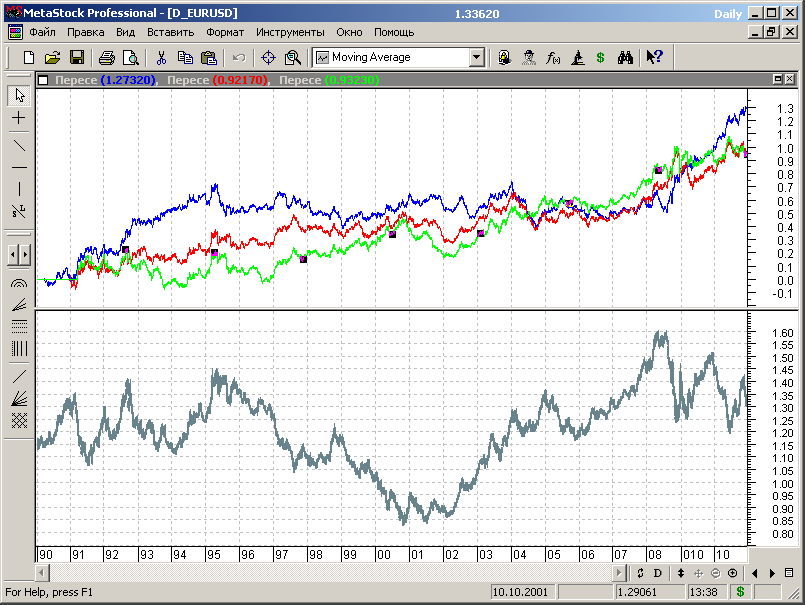
Рис.7.4.
Оптимум для периода 40 сохранился, также как сохранилась и неудовлетворительная работа стратегии в большей части диапазона.
Оптимум 130 сдвинулся до 120, а оптимум 270 переместился в зону 275. Т.е. параметры стратегии в целом остаются стабильными, чего не скажешь о результатах.
7.5.1. Торговая идея.
В предыдущем примере использовали самый простой принцип применения МТС на основе скользящей средней, взятый в чистом виде. Да, принципиально он работает, как и большинство индикаторных методов ТА, но проблемы, как всегда, кроются в деталях и нюансах. А один из нюансов рассмотренного примера – это тот факт, что такого рода стратегии плохо работают на рынках, где нет выраженного тренда. Они открывают множество встречных сделок на «шумовых» движениях цены, теряя при этом прибыль, накопленную на трендовых участках рынка.
Частично устранить этот недостаток можно используя пересечение двух скользящих средних, одна которых, более быстрая с меньшим периодом, представляет собой сглаженный эквивалент графика цены, а вторая, более медленная, используется для определения направления тренда.
Выбором соотношения между периодами МА можно уменьшить количество «ложных» срабатываний МТС за счет шумовых компонент движения цены, а также уменьшить количество сделок на участках рынка с боковом трендом (рис.7.5).
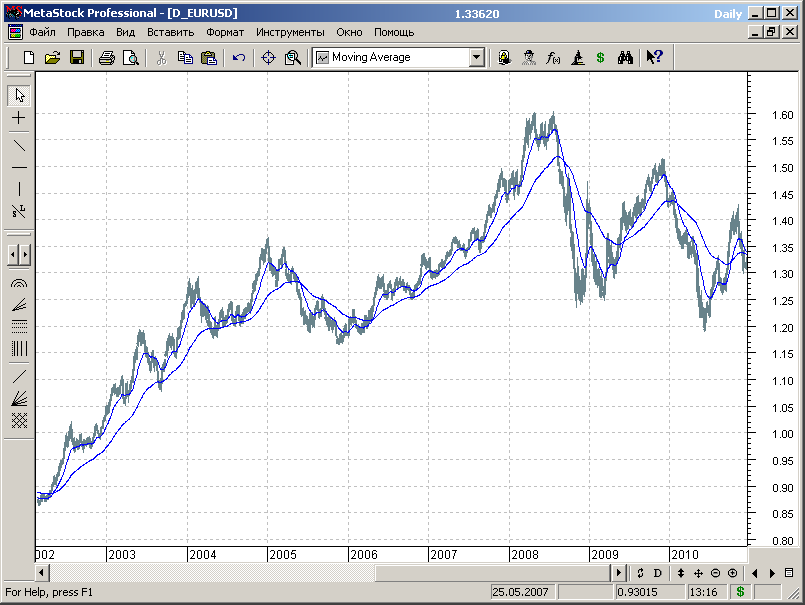
Рис.7.5.
Торговая идея для этого случая тоже очень проста: если быстрая скользящая средняя расположена выше медленной МА, то тренд восходящий, а если ниже - нисходящий. Соответственно, точки пересечения быстрой и медленной МА считаются точками перемены направления тенденции и используются в качестве торговых сигналов МТС.
Торговые правила для оптимизируемой торговой стратегии на основе пересечения двух скользящих средних будут иметь вид:
Buy Order: Cross(Mov(C,opt2,E),Mov(C,opt1,E))
Sell Order: Cross(Mov(C,opt1,E), Mov(C,opt2,E))
Sell Short Order: Cross(Mov(C,opt1,E), Mov(C,opt2,E))
Buy to Cover Order: Cross(Mov(C,opt2,E),Mov(C,opt1,E))
В записанных торговых правилах мы предположили, что скользящая средняя с оптимизационной переменной opt2 является «быстрой» скользящей средней в рамках используемой торговой идеи.
Отметим, что мы, как правило, используем экспоненциальную скользящую среднюю, но с таким же успехом можно тестировать стратегии и на других типах скользящих средних, поддерживаемых программой Метасток.
Открываем тестер систем, и строим новую торговую систему с вышеуказанными торговыми правилами.
Для первоначальной оптимизации в пределах стартового сегмента зададим диапазоны переменных оптимизации:
- для медленной скользящей средней диапазон opt1 от 10 до 300 с шагом 5;
- для быстрой – диапазон opt2 от 3 до 150 с шагом 3.
Теперь можно приступать к тестированию и оптимизации системы.
P.S. Комбинаций многовато, 1770, но проведем тест, а потом будем смотреть.
Запускаем тест на стартовом сегменте исторических данных.
Отметим, что анализ результатов, когда оптимизация идет более чем по одному параметру, проводить гораздо сложнее, чем в случае одного параметра – трудно визуально ценить оптимумы по нескольким переменным одновременно. Для двух переменных в этом случае помогло бы трехмерное отображение результатов тестирования, но к сожалению Метасток такой возможности нам не предоставляет. Поэтому будем пользоваться тем, что есть, а есть у нас диаграмма с результатами тестирования, которая представлена на рисунке 7.6.
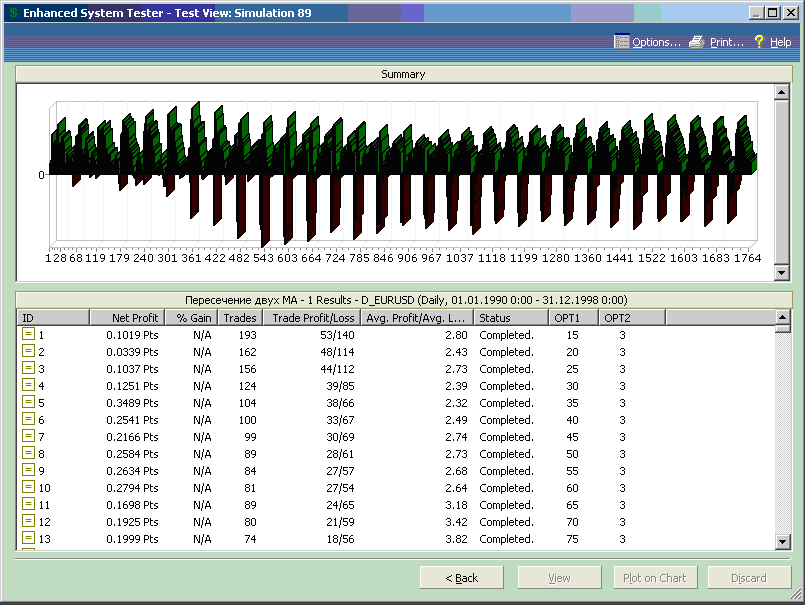
Рис.7.6.
При первом взгляде на эту диаграмму трудно сказать что-либо определенное, кроме того, что в предложенной комбинации есть и прибыльные тесты и убыточные, причем во всем диапазоне изменения данных.
Наличие прибыльных и убыточных тестов закономерно, так как мы при записи торговых правил теста не налагали никаких ограничений на соотношение параметров двух скользящих средних. Так что «быстрая» МА могла иметь в некоторых комбинациях теста больший период, чем «медленная», в некоторых они могли просто совпасть, не давая никаких сигналов.
Что же полезного можно почерпнуть из представленной диаграммы?
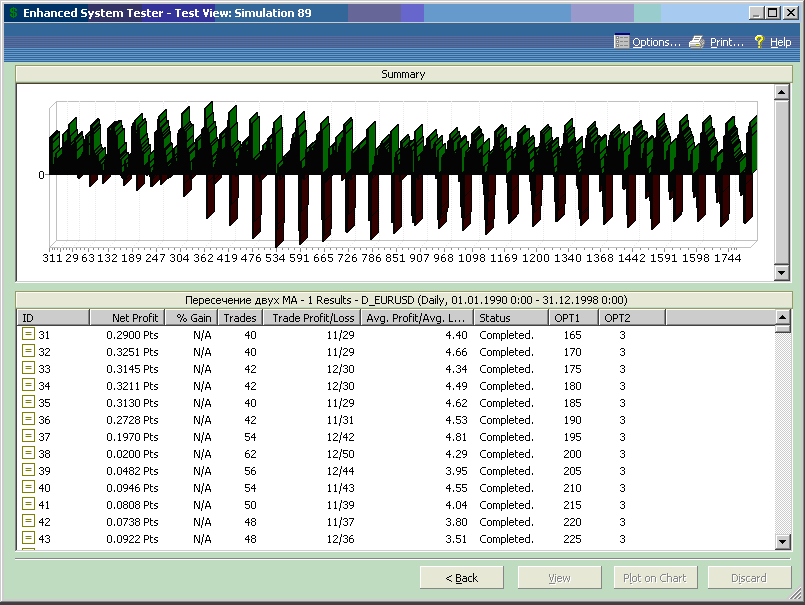
Рис.7.7.
Для параметра opt2 наблюдается два оптимума, первый в зоне малых значений переменной, второй – в зоне больших, но в зоне малых значений opt2 удельный вес убыточных сделок меньше, тогда как в зоне большиз значений их количество возрастает. Возможно, в силу специфики записи торговых условий теста это проявляются комбинации, при которых быстрая и медленная МА меняются местами.
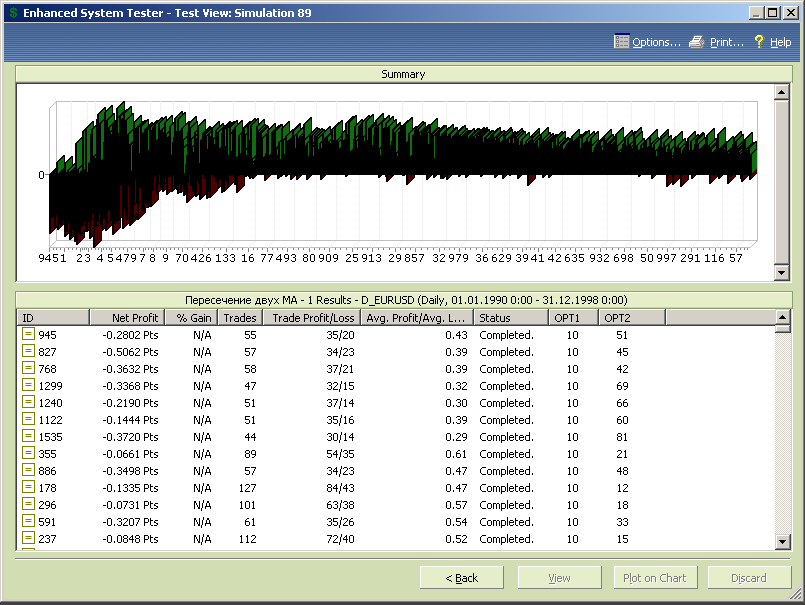
Рис.7.8.
Зона оптимальных параметра opt1 значений расположена в диапазоне значений начиная от 25 и выше. С ростом периода МА идет повышение максимумов профитных тестов, а затем постепенный спад. В зоне максимумов расположены и наихудшие тесты.
Упорядочим тесты по размеру профита (рис.7.9) и убытка (рис.7.10).
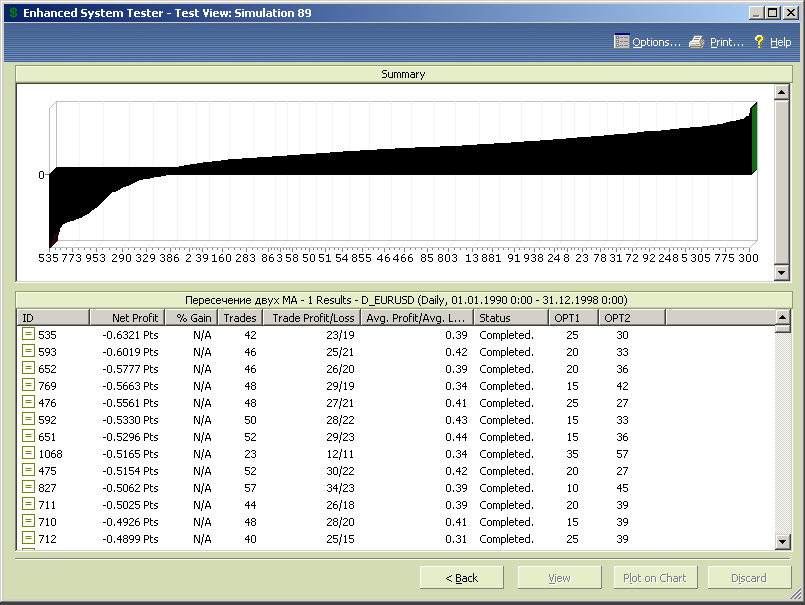
Рис.7.9.
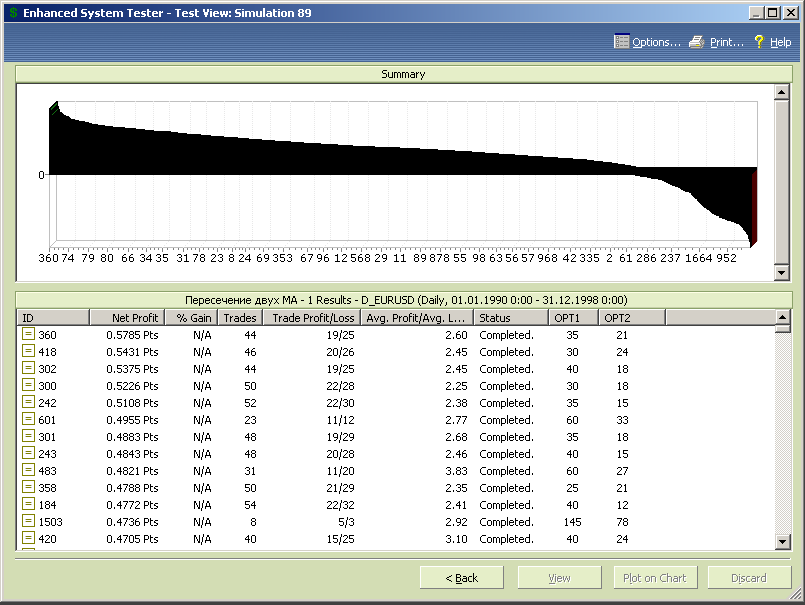
Рис.7.10.
Вот теперь видно, что прибыльных комбинаций все-таки больше, чем убыточных.
Также проявился тот факт, что наиболее прибыльные тесты получаем в случае, когда у нас «правильное» соотношение периодов МА, т.е. период «медленной» скользящей средней больше периода «быстрой» скользящей средней, а максимальный убыток идет при обратном соотношении периодов.
Но все-таки корректно выделить тесты для продолжения исследований из полученного материала пока что трудно из-за недостаточной системности в изменении параметров торговой стратегии. Для устранения этого недостатка попробуем модифицировать торговые правила.
Запишем торговые правила в виде, который исключает инверсное расположение скользящих средних, т.е. так, чтобы быстрая МА всегда была быстрой, медленная МА – медленной, а кобинации с обратным расположением скользящих средних исключались.
Один из вариантов такой записи сводится к тому, что период быстрой скользящей средней вычисляется умножением периода медленной скользящей средней на множитель, который меньше единицы. Торговые правила для этого случая будут иметь вид:
Buy Order: Cross(Mov(C,0.01*opt2*opt1,E),Mov(C,opt1,E))
Sell Order: Cross(Mov(C,opt1,E), Mov(C,0.01*opt2*opt1,E))
Sell Short Order: Cross(Mov(C,opt1,E), Mov(C,0.01*opt2*opt1,E))
Buy to Cover Order: Cross(Mov(C,0.01*opt2*opt1,E),Mov(C,opt1,E))
Для первоначальной оптимизации в пределах стартового сегмента зададим диапазоны переменных оптимизации:
- для медленной скользящей средней диапазон opt1 от 10 до 200 с шагом 5;
- для быстрой – диапазон opt2 от 1 до 50 с шагом 1.
Таким образом, период быстрой МА будет изменяться от 0.01 до 0.5 периода медленной МА.
Здесь есть два момента, на которые следует обратить внимание.
Первое – период скользящей средней в Метасток может быть только целым числом, а в результате вычислений будут получаться и дробные значения периодов. Встроенная формула для пользовательского индикатора скользящей средней допускает ввод как целых, так и дробных величин, определяющих значения периода, в последнем случае программа просто отбрасывает дробную часть введенного числа. Поэтому значения периодов, например, 7.0 и 7.6 будут эквиваленты, и оба будут обрабатываться при вычислении МА как число 7.
И второе. Следствием предыдущего замечания является то, что комбинации 0.01*opt2*opt1, результат которых будет меньше единицы, будут обрабатываться как ноль, давая ошибки при проведении теста. Эти ошибочные результаты мы просто отбросим при анализе результатов тестирования.
Открываем тестер систем, и строим новую торговую систему с модифицированными торговыми правилами.
P.S. Вариант записи 0.01*opt2 вместо использования дробных значений opt2 использован потому, что при обработке диапазона дробных значений переменной оптимизации тестер иногда расширяет диапазон переменной на один шаг.
Запускаем тест на стартовом сегменте исторических данных.
Диаграмма результатов тестирования представлены на диаграмме рисунка 7.11.
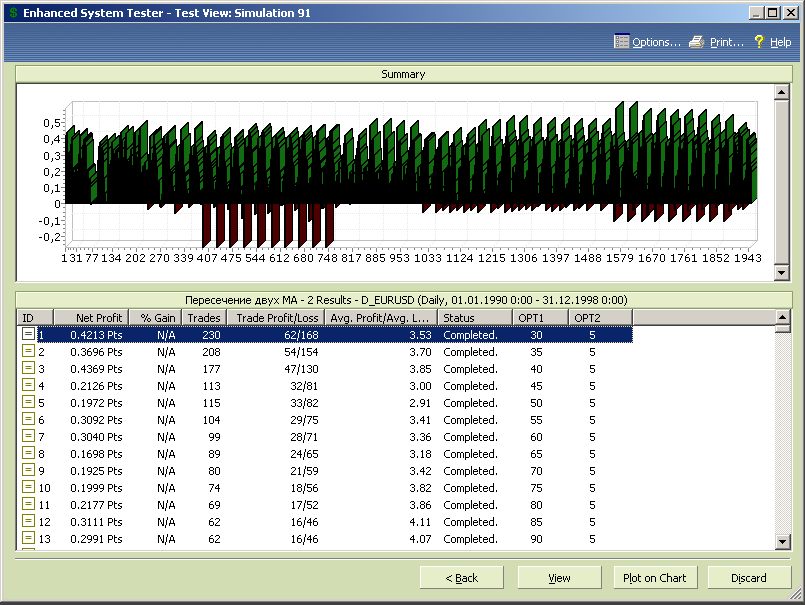
Рис.7.11.
На основе полученных данных можно сделать предварительный вывод, что данная МТС дает больше прибыльных комбинаций, чем убыточных. Для получения более детальной оценки характеристик системы перейдем к подробному анализу влияния параметров оптимизации на ее характеристики. Однако предварительно исключим из результатов тестирования тесты, которые прошли с ошибкой из-за равенства периодов обеих скользящих средних. Такие тесты характеризуются нулевым количеством сделок или комментарием «Had errors» в колонке «Status».
Упорядочиваем тесты по количеству сделок или по параметру «Status», чтобы сгруппировать некорректные тесты (см.рис.7.12).
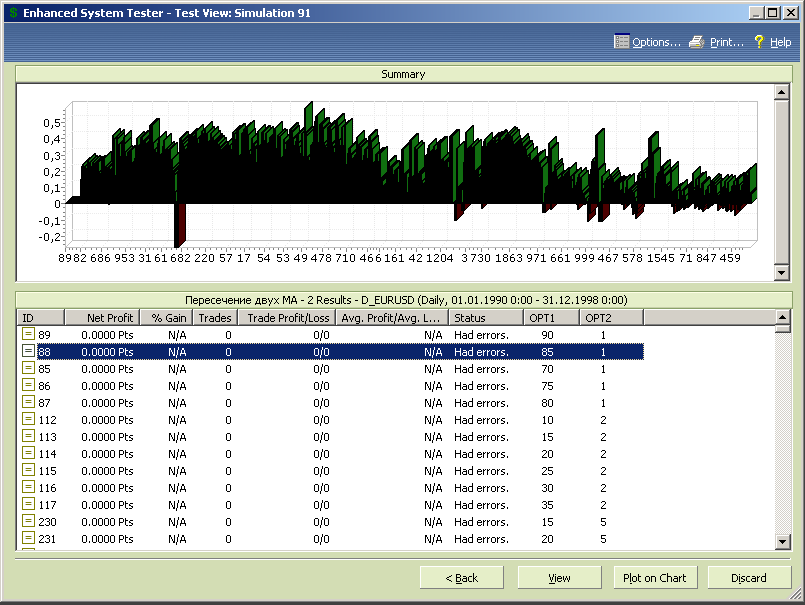
Рис.7.12.
С помощью нажатия клавиши Ctrl или Shift и указателя мышки выделяем тесты с ошибкой и нажимаем клавишу «Discard», удаляя некорректные тесты из общих результатов тестирования.
Оставшиеся тесты проанализируем по параметрам opt1 и opt2.
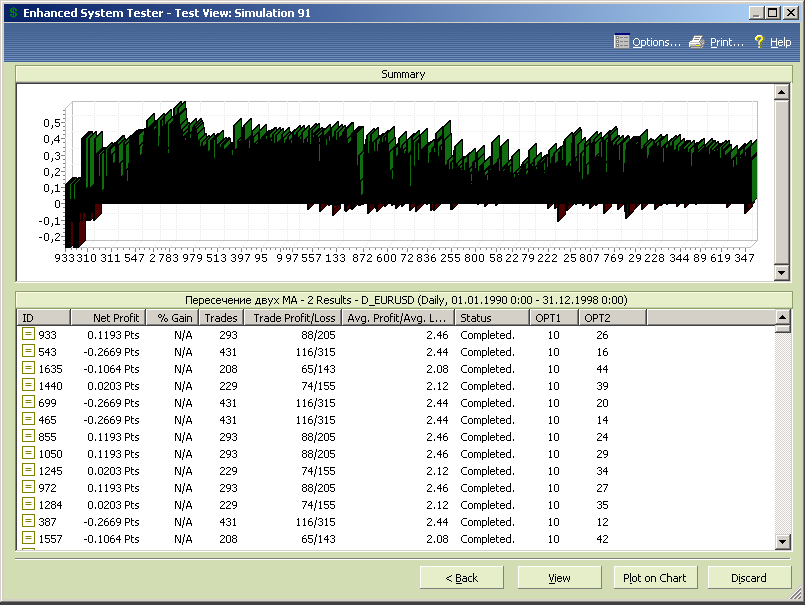
Рис.7.13.
Анализ представленных данных показывает, что имеется зона оптимума значений переменной opt1, ограниченная значениями примерно от 20 до 100, в пределах которой находятся наиболее прибыльные тесты и практически нет убыточных комбинаций параметров opt1 и opt2. При уходе из этой зоны вниз, в зону меньших значений, резко возрастает количество убыточных стратегий и величины получаемых убытков. При уходе вверх постепенно спадает и размер полученной прибыли, и количество сделок на тестируемом диапазоне данных, что уменьшает статистическую достоверность результатов тестирования.
Изменим диапазон переменной opt1, ограничив его величинами 20 и 100, и повторим тест.
Также увеличим до 5 нижнюю границу диапазона изменения opt2, чтобы уменьшить количество тестов с ошибкой из-за нулевых значений периода быстрой скользящей средней.
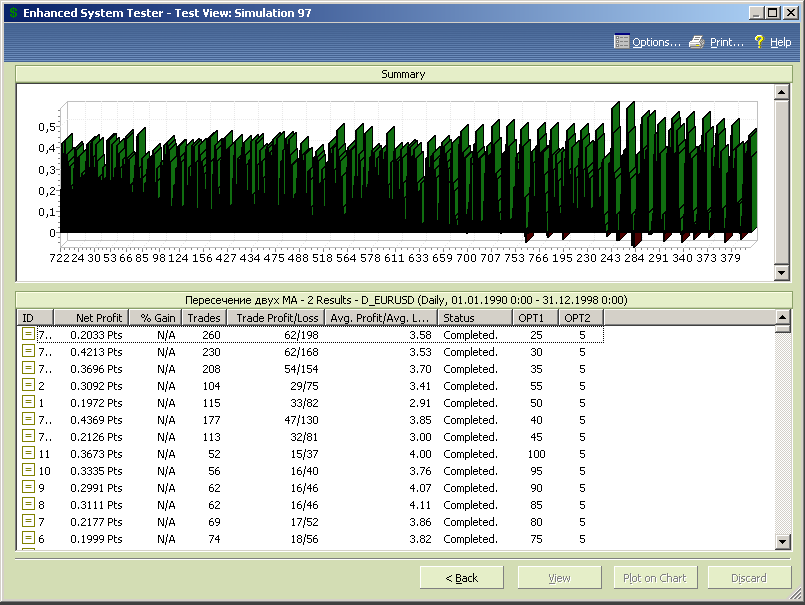
Рис.7.14.
Анализ представленных данных показывает, что с ростом переменной opt2 прибыльность тестов в среднем возрастает, но возрастает и чувствительность результатов тестирования к изменению соотношения периодов скользящих средних, что выражается в более глубоких провалах между оптимумами теста.
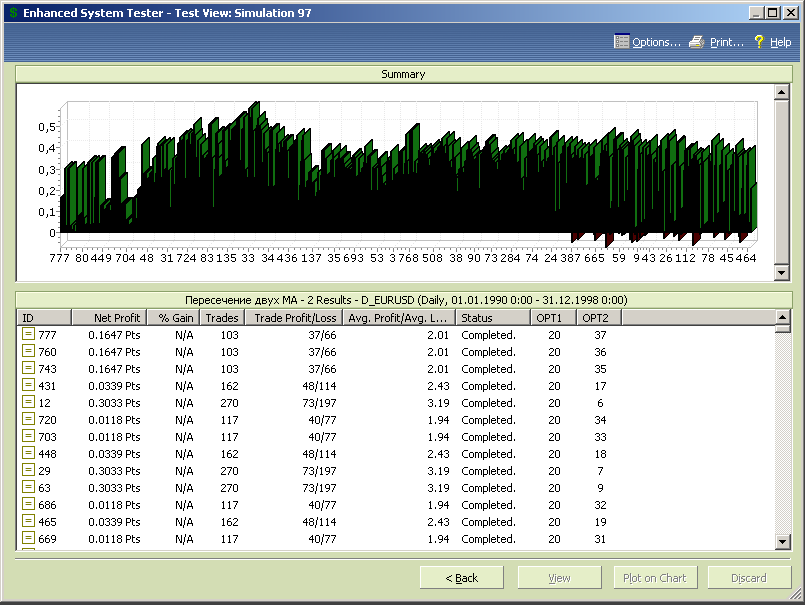
Рис.7.15.
Еще раз «обрежем» диапазон изменения opt1, установив его границы от 25 до 55 с шагом 1, и проведем тестирование стратегии.
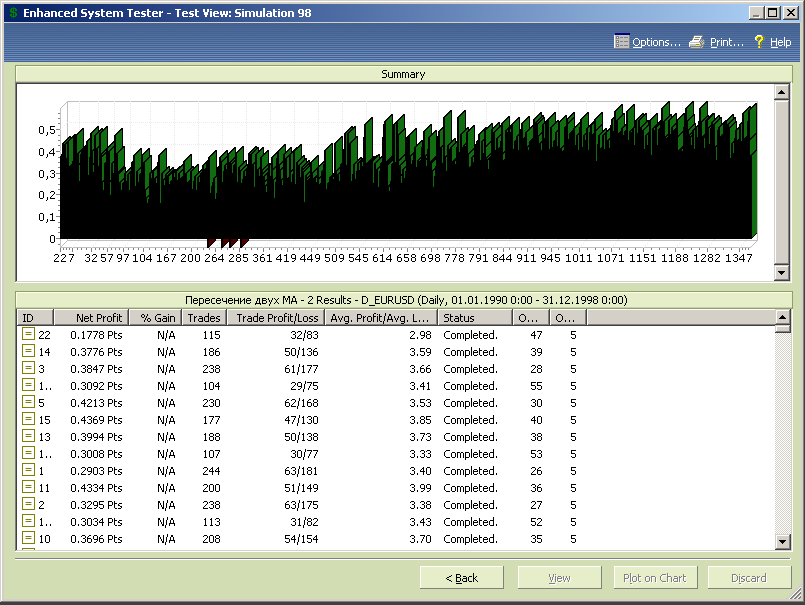
Рис.7.16.
Проводим тестирование и смотрим результаты.
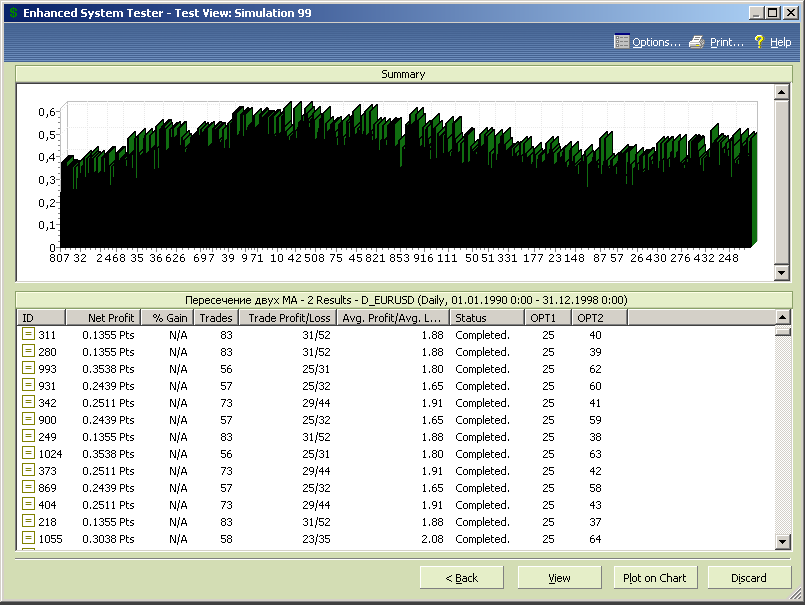
Рис.7.17.
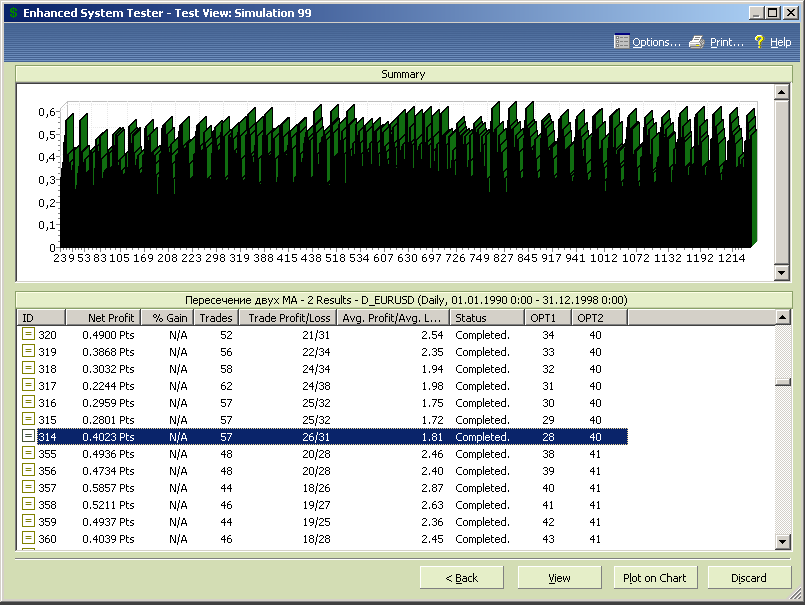
Рис.7.18.
Задаем новые диапазоны изменения оптимизационных переменных и продолжаем первоначальную оптимизацию.
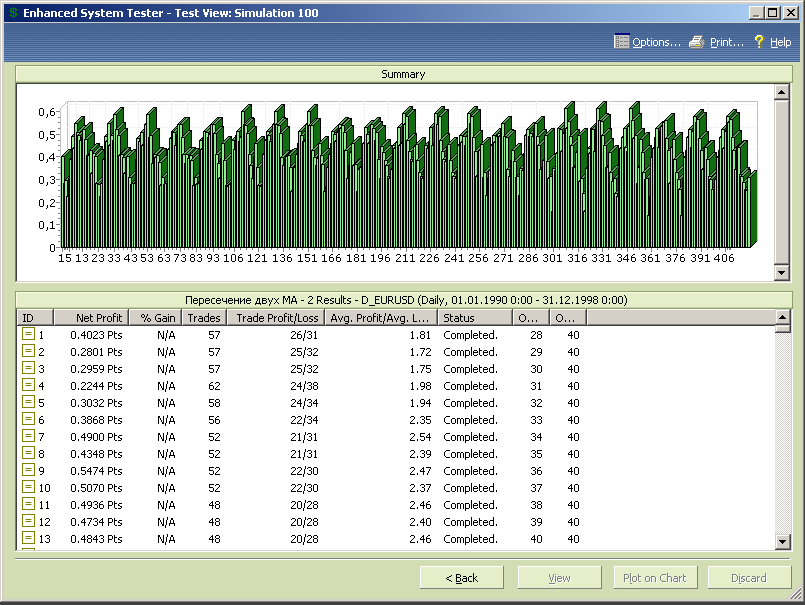
Рис.7.19.
Явных провалов на диаграмме не наблюдается, т.е. стратегия при заданных диапазонах переменных в целом показывает прибыльную работу. Займемся частностями и деталями.
Переменная opt2 при этом принимает значения в окрестности 50, т.е. оптимальное соотношение периодов быстрой и медленной скользящих средних для данного финансового инструмента и для данного диапазона исторических данных примерно равно 2.
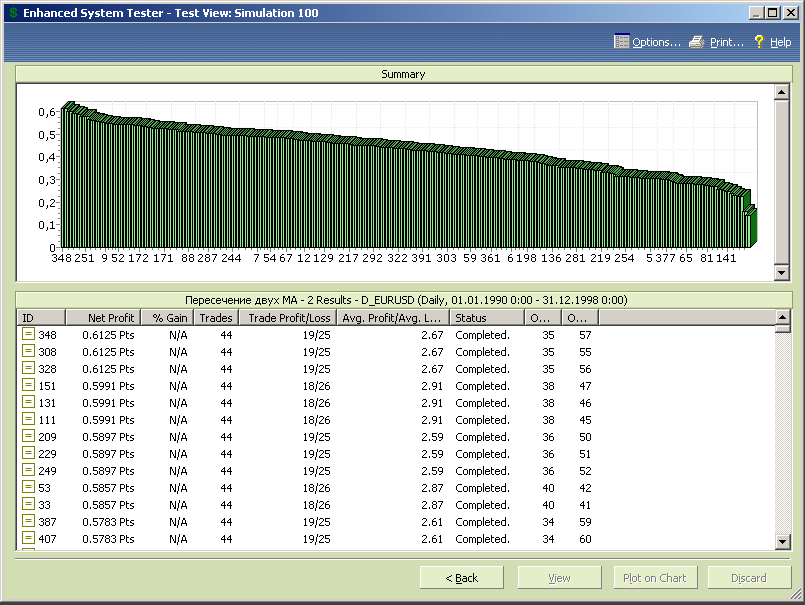
Рис.7.20.
Для значения переменной opt1=35 больше прибыль и процент прибыльных сделок. Для значения opt1=38 больше соотношение средней прибыли к среднему убытку.
Окончательный выбор той или иной стратегии можно сделать по результатам анализа линий эквити, представленных на графиках рисунка 7.21.
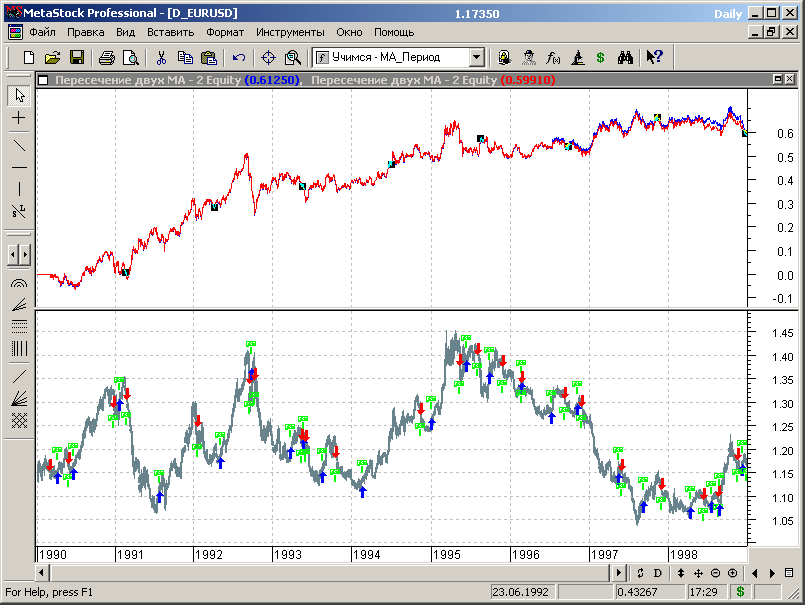
Рис.7.21.
Сравнительный анализ линий эквити показывает почти полную идентичность обеих торговых стратегий, за исключением незначительных деталей на последнем участке.
Обе стратегии хорошо работают на участках выраженного тренда, как восходящего, так и нисходящего, и обе не дают прибыли, но и не приносят убытка на участках бокового (или близкого к боковому) трендов. На двух участках экстремальных провалов в 1992 и 1195 годах ситуацию, вероятнее всего, можно улучшить с помощью ордеров стоп-лосс, ограничивающих убытки в сделке. К этому вопросу мы вернемся позже, в разделе, посвященном системам с раздельными выходами.
Для последующего анализа на данных «вне-выборки» и проведения процедуры циклической оптимизации в соответствии с алгоритмом, изложенным в подразделе 6.7 на примере канальных стратегий, можно выбрать любую из представленных стратегий.
Следует отметить, что только при циклической оптимизации можно получить достоверные оценки характеристики оптимизированной торговой стратегии для работы в реальном времени, причем исключительно на данных, расположенных «вне-выборки», которая использовалась для оптимизации в каждом цикле. Как это сделать, показано в подразделе 6.7. Мы же только проверим, сохранятся ли полученные на этапе первоначальной оптимизации параметры МТС на диапазоне исторических данных, включающих все сегменты.
Диаграмма результатов теста на всей совокупности сегментированных исторических данных представлена на рисунке 7.22.
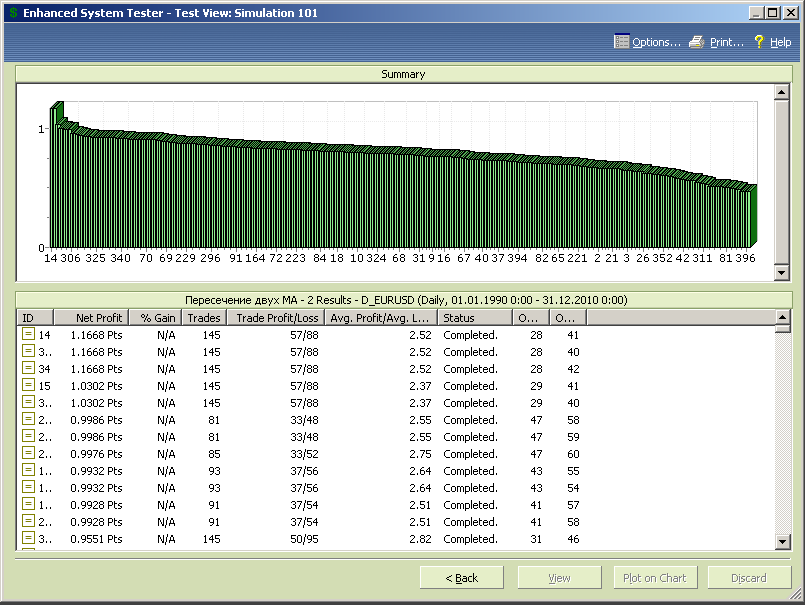
Рис.7.22.
Анализ полученных результатов показывает, что характеристики рынка со временем изменились. Оптимальными стали более быстрые стратегии, с меньшим периодом «медленной» МА и большим отношением периодов «быстрой» и «медленной» МА. Но на арену также вышли и медленные стратегии, в которых значение периода «медленной» МА возросло относительно результатов, полученных на этапе первоначальной оптимизации. По сути, первоначальная МТС распалась на две отдельных стратегии с различными параметрами.
Представленные данные еще раз иллюстрируют необходимость проведения исследований стратегии методом циклической оптимизации. В этом случае параметры стратегии постепенно подстраивались бы к изменяющимся свойствам рынка, обеспечивая пошагового согласование и настройку параметров МТС на текущую динамику рынка, а оценка поведения МТС на данных «вне выборки» показала бы, какие сюрпризы могут нас ожидать в будущем.
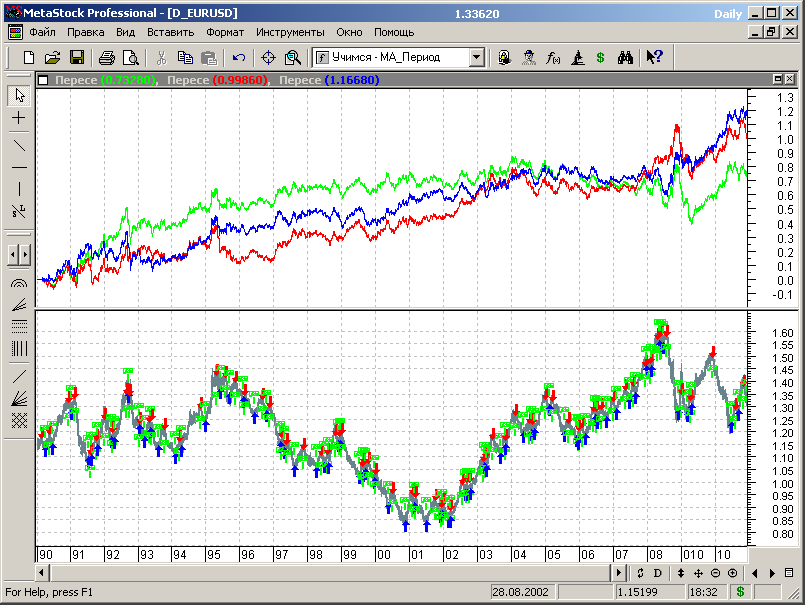
Рис.7.23.
Зеленым цветом показана «оптимальная» стратегия по результатам первоначальной оптимизации, а красным и синим цветами соответственно медленная и быстрая стратегии по результатам теста на всей совокупности сегментированных данных.
Из представленных графиков можно видеть, что первоначальная стратегия сохраняла работоспособность и прибыльность на протяжении примерно 5-6 лет после оптимизации, а затем начала постепенно уходить в убытки и перешла на участок колебательного характера эквити с высокой волатильностью.
Быстрая стратегия показывает наилучшие результаты на представленном диапазоне данных, а медленная несколько хуже в прошлом и сравнимые показатели с быстрой стратегией на последнем сегменте.
Указанные обстоятельства еще раз подтверждают необходимость циклической настройки стратегий, а оптимальный период цикла и результативность метода могут быть выявлены только на данных «вне выборки» в процессе циклической оптимизации.
Конечно, можно взять весь диапазон исторических данных сразу и оптимизировать на нем свою МТС. Но в этом случае у нас не будет никаких более-менее объективных сведений о возможном поведении торговой стратегии в будущем, и информации о том, как часто, с какой периодичностью и на каком интервале данных нужно подстраивать параметры МТС под параметры рынка.
Отметим, что провалы 2008 года для всех стратегий, появившиеся на воне финансового кризиса 2008 года, характерны для всех механических систем при явлениях катастрофического характера, а кризис был катастрофой, которая изменила характер всех рынков. Способ борьбы с такого рода явлениями один – «антикатастрофические» ордера стоп-лосс, которые расположены за пределами «обычной» волатильности рынка.
7.6.1. Торговая идея.
Еще один способ применения скользящих средних основан на использовании пересечения МА и смещенного вперед (назад) скользящего среднего с теми же параметрами.
В этом случае сигнал на покупку возникает, когда исходное МА поднимается выше смещенного скользящего среднего, а сигнал на продажу – когда исходное среднее опускается ниже смещенного. Выбором величины сдвига можно уменьшить количество ложных пересечений, уменьшая частоту убыточных сигналов.
Вариантом этого метода является метод, использующий пересечение графика цены со сдвинутой МА, или графика цены со сдвинутым вперед графиком цены. Следует отметить, что последний вариант (используемый, кстати, и в популярном индикаторе Ишимоку) представляет собой не что иное, как другую запись индикатора моментум, рассмотренного нами в подразделе 4.6, пункт 4.6.2.
График цены в совокупности со сдвинутыми вперед скользящими средними используется также в торговой системе Б. Вильямса.
Торговые правила для оптимизируемой торговой стратегии на основе пересечения скользящей средней со сдвинутой вперед скользящей средней такого же периода будут иметь вид:
Buy Order: Cross(Mov(C,opt1,E), Mov(ref(C,-opt2),opt1,E))
Sell Order: Cross(Mov(ref(C,-opt2),opt1,E),Mov(C,opt1,E))
Sell Short Order: Cross(Mov(ref(C,-opt2),opt1,E),Mov(C,opt1,E))
Buy to Cover Order: Cross(Mov(C,opt1,E), Mov(ref(C,-opt2),opt1,E))
Здесь у нас два параметра оптимизации, а именно: период скользящей средней и величина сдвига. Мы по-прежнему используем экспоненциальную скользящую среднюю, для других типов построение теста и проведение процедуры тестирования будет аналогичным, необходимо только изменить обозначения типа скользящей средней в формулах.
Открываем тестер систем, и строим новую торговую систему с вышеуказанными торговыми правилами.
Для первоначальной оптимизации в пределах стартового сегмента зададим диапазоны переменных оптимизации:
- период скользящей средней, определяемой переменной оптимизации opt1, в диапазоне от 10 до 200 с шагом 5;
- величину сдвига, определяемую переменной оптимизации opt2, от 2 до 50 с шагом 2.
Приступаем к тестированию и первоначальной оптимизации системы.
Запускаем тест на стартовом сегменте исторических данных.
Результаты первоначально оптимизации, представленные на диаграмме рисунка 7.24, достаточно интересны.
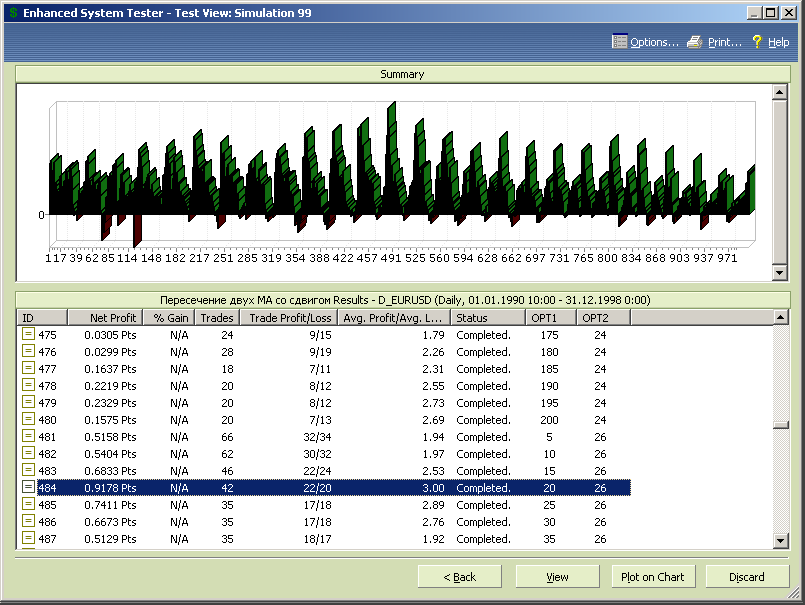
Рис.7.24.
Во-первых, прибыльность тестируемой стратегии на стартовом сегменте примерно на 40% выше, чем у МТС, основанной на пересечении двух скользящих средних, которую мы рассматривали в предыдущем подразделе.
Во-вторых, на диаграмме прослеживается явная цикличность, которая показывает, что для каждого периода скользящей средней есть свой оптимальный сдвиг.
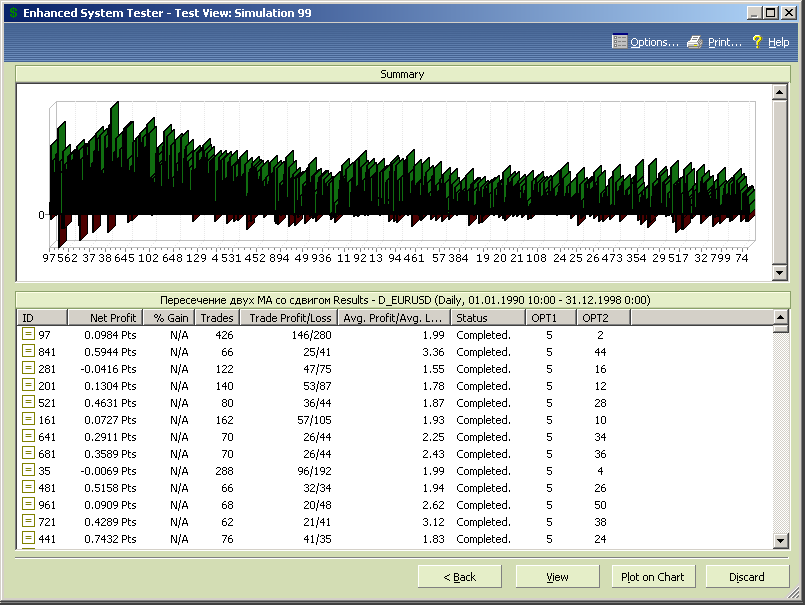
Рис.7.25.
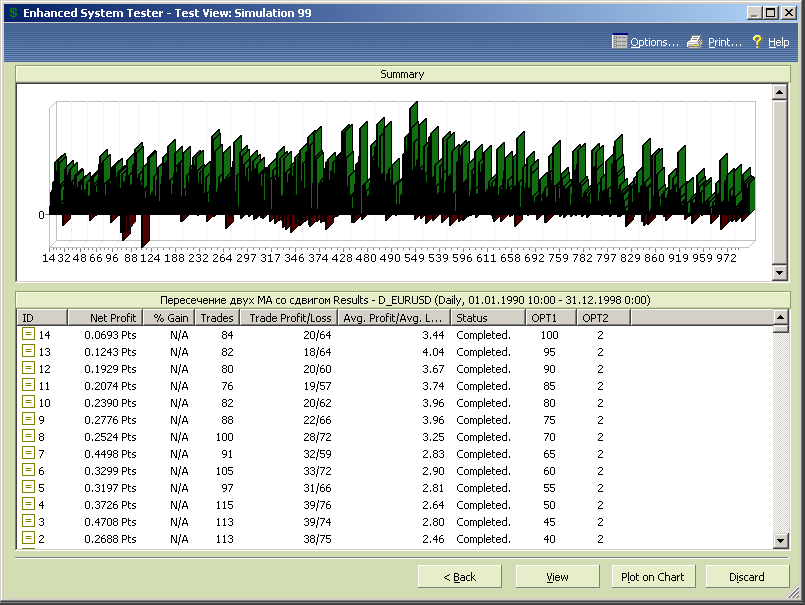
Рис.7.26.
Перед тем, как ограничивать диапазоны изменения оптимизационных переменных и приступать к дальнейшему тестированию стратегии с целью выделения зон оптимума параметров МТС, проверим еще одно обстоятельство.
В рассмотренном примере величина сдвига и период скользящей средней изменяются независимым образом. Возможно, это и правильно, но интуитивно кажется более верным, что чем оптимальный сдвиг должен быть пропорционален периоду скользящей, так как сдвиг 50 для периода 20 и сдвиг 50 для периода 200 неэквивалентны и работают на принципиально разных свойствах МА. В детали этого вдаваться не будем, но попробуем модифицировать торговые правила таким образом, чтобы сдвиг задавался в величинах, пропорциональных периоду скользящей средней.
Модификация торговых правил для этого случая будет иметь вид:
Buy Order: Cross(Mov(C,opt1,E), Mov(ref(C,-0.01*opt2*opt1),opt1,E))
Sell Order: Cross(Mov(ref(C,-0.01*opt2*opt1),opt1,E),Mov(C,opt1,E))
Sell Short Order: Cross(Mov(ref(C,-0.01*opt2*opt1),opt1,E),Mov(C,opt1,E))
Buy to Cover Order: Cross(Mov(C,opt1,E), Mov(ref(C,-0.01*opt2*opt1),opt1,E))
У нас по-прежнему два параметра оптимизации, но степень свободы стратегии уменьшена, поскольку величина сдвига уже зависит от значения периода скользящей средней.
Зададим диапазоны переменных оптимизации:
- период скользящей средней, определяемой переменной оптимизации opt1, в диапазоне от 10 до 100 с шагом 5;
- значения переменной оптимизации opt2, определяющей величину сдвига, будем изменять от 5 до 200 с шагом 5.
Следует отметить, что мы сознательно задали возможный диапазон сдвига больше периода скользящей средней, поскольку оптимум теста, результаты которого представлены на рисунке 7.24, расположен в зоне сдвигов, больших, чем период МА.
Открываем тестер систем, строим новую торговую систему и приступаем к тестированию и первоначальной оптимизации системы.
Из диаграммы результатов теста, представленной на рисунке 7.27, следует, что принципиальных отличий в результатах теста, на первый взгляд, нет, а оптимум сохранился на тех же значения периода и сдвига.
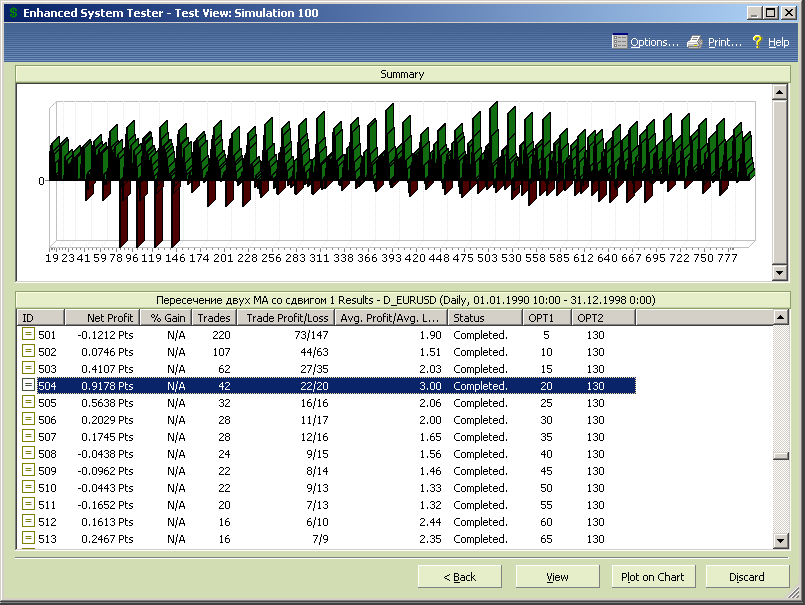
Рис.7.27.
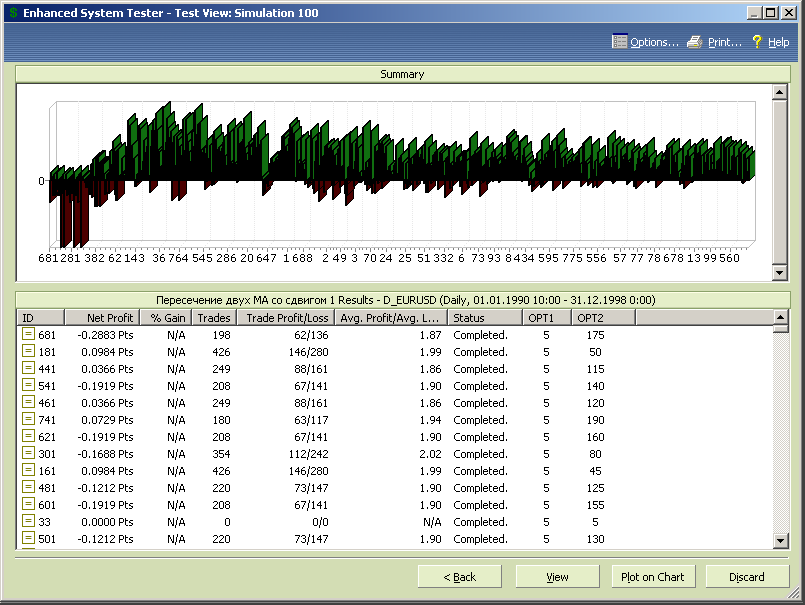
Рис.7.28.
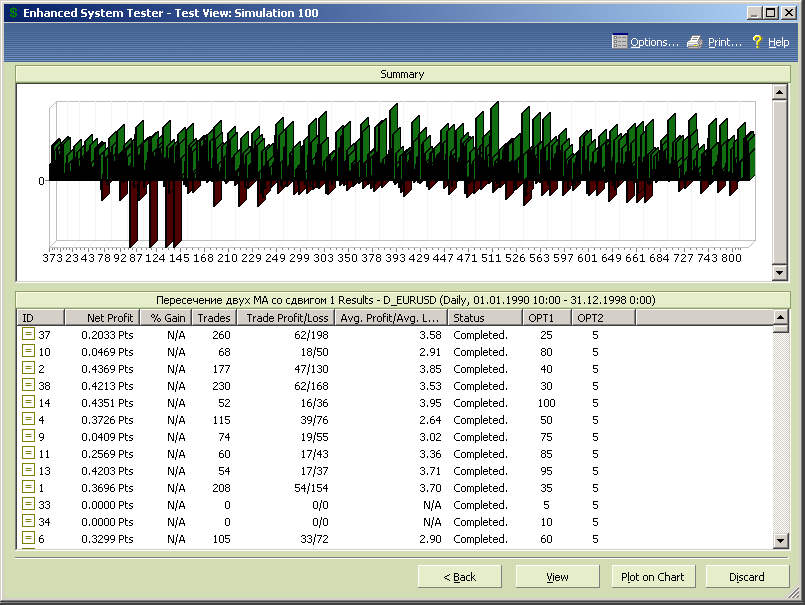
Рис.7.29.
Корректируем диапазоны переменных, задавая значения opt1 от 16 до 50 с шагом 2, а opt2 от 100 до 200 с шагом 2 и проводим новый этап первоначальной оптимизации системы.
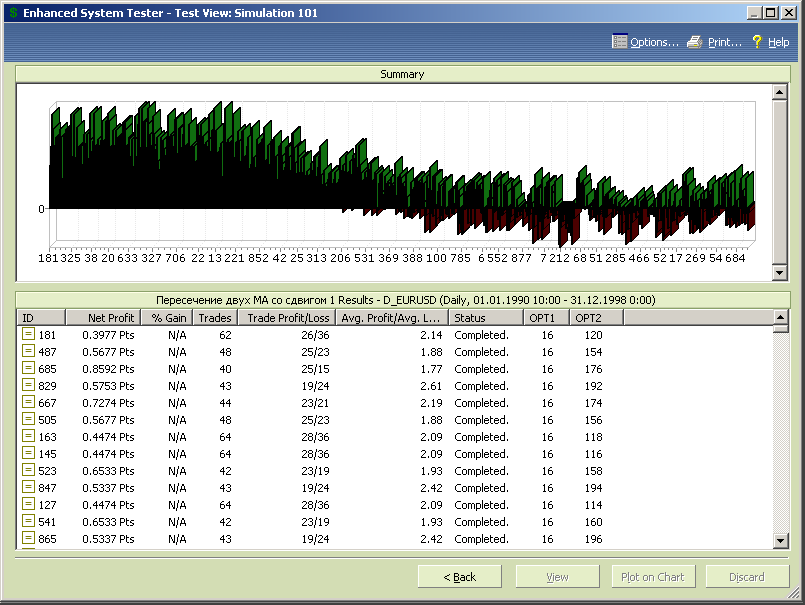
Рис.7.30.
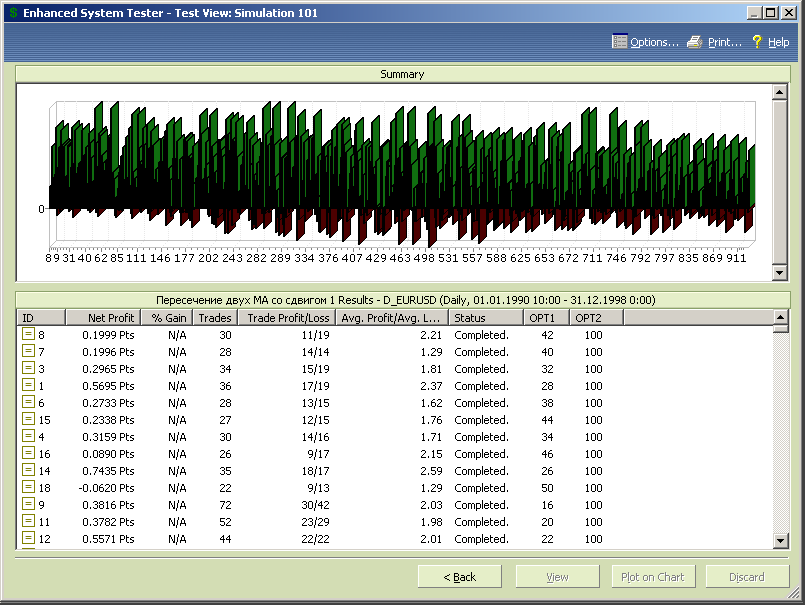
Рис.7.31
Корректируем диапазон переменной opt1, задавая его границы от 15 до 30 с шагом 1 при неизменном диапазоне значений opt2, и проводим новый тест.
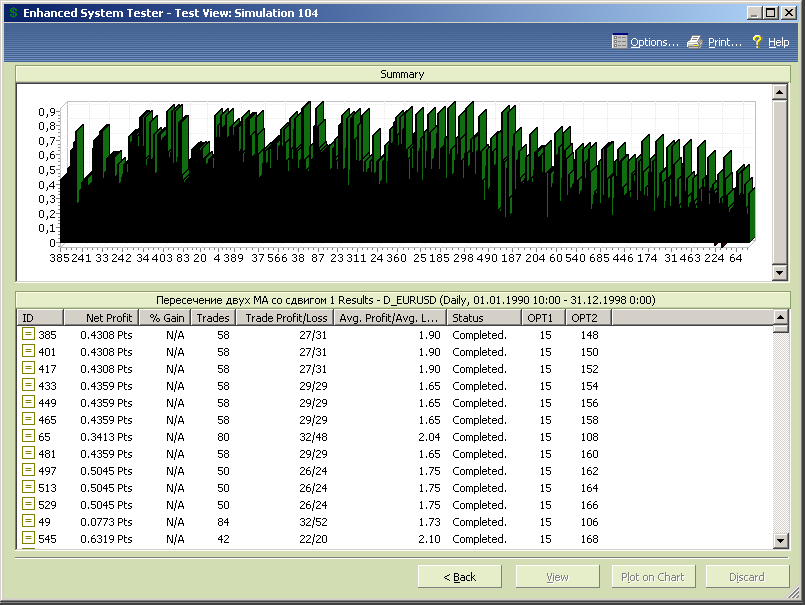
Рис.7.32.
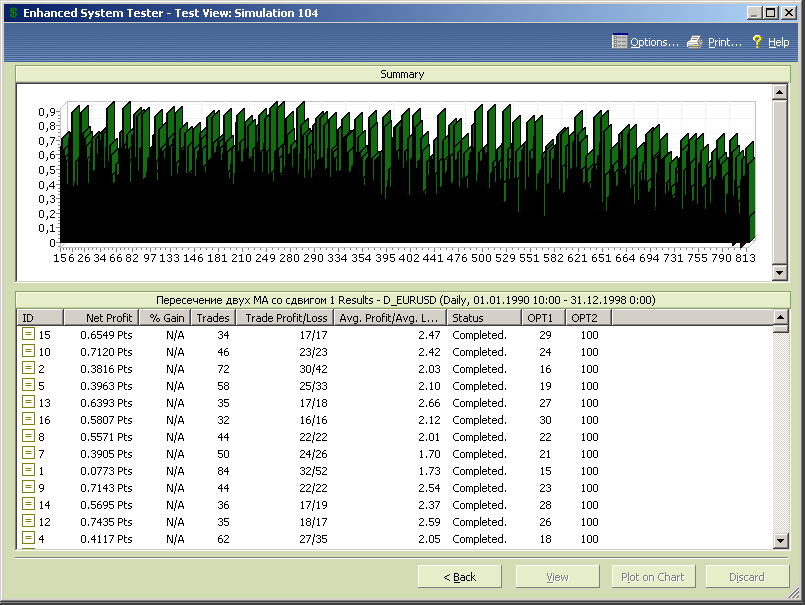
Рис.7.33.
Попробуем уменьшить количество избыточной информации в диаграммах за счет перехода к первоначальной версии стратегии, но с уточненными диапазонами переменных. Диапазон opt1 будет принимать значения от 15 до 30 с шагом 1, а диапазон opt2 от 15 до 60 с шагом 1, что охватывает весь возможный диапазон тестов модифицированной стратегии, устраняя избыточные.
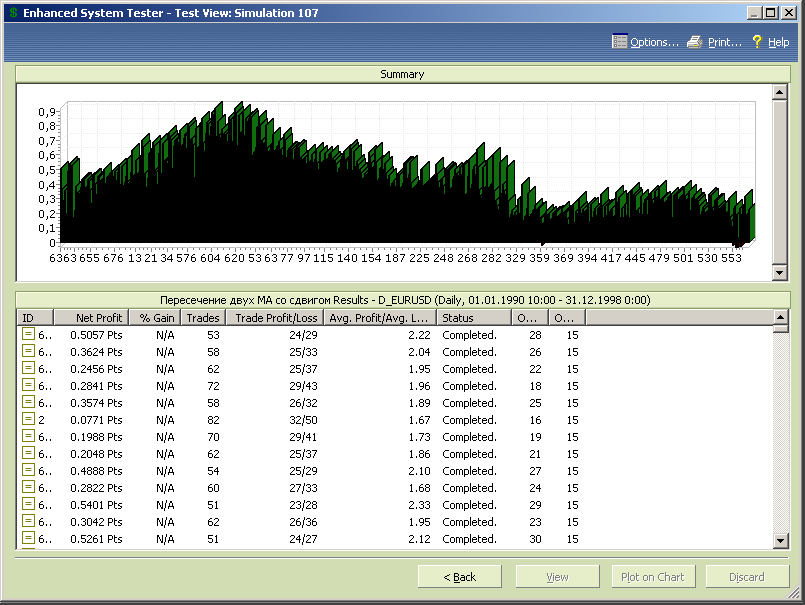
Рис.7.34.
Что можно сказать. По периоду скользящей средней выраженных оптимумов нет, поэтому мы эту диаграмму не приводим. А на представленном графике данные упорядочены по росту сдвига и из этого рисунка следует, что наше предположение о том, что сдвиг должен быть пропорционален периоду скользящей средней, все-таки не совсем верно.
Из представленной диаграммы следует, что верхнюю половину диапазона изменения сдвига можно отбросить, оставив значения параметра opt2 примерно до 35.
Кроме того, можно удалить часть значений снизу, до17 включительно.
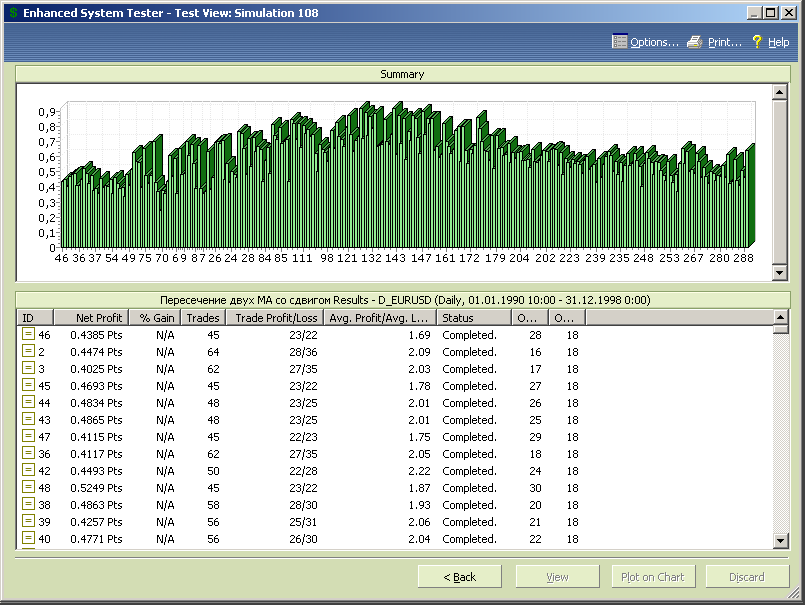
Рис.7.35.
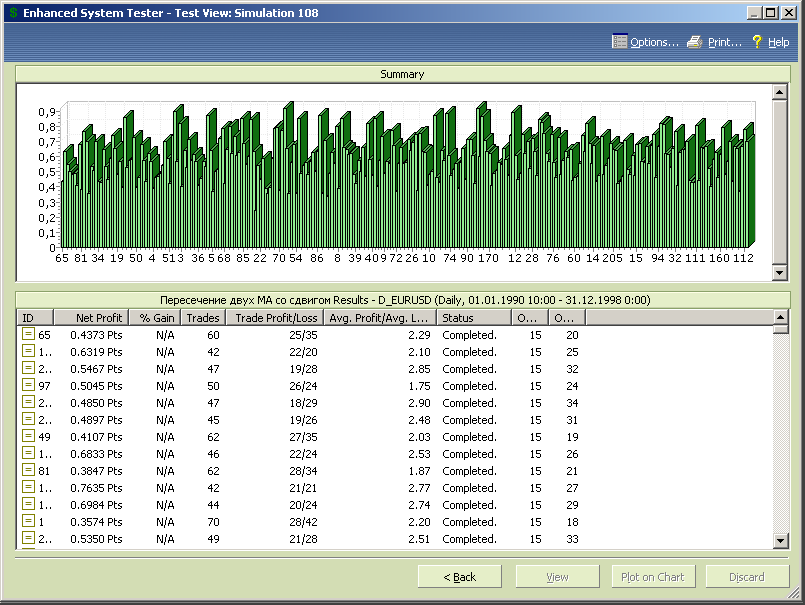
Рис.7.36.
Оптимальная стратегия обеспечивает на интервале тестируемых данных почти 92 фигуры профита (9178пп), процент прибыльных сделок больше 52%, отношение средней прибыли к среднему убытку в окрестности 3.0, а значение параметра профит-фактор выше 3.3. Т.е. объективные параметры стратегии вполне удовлетворительные, даже можно сказать, хорошие.
Поведение линии эквити (рис.7.38) показывает небольшой локальный провал на начальном участке диапазона тестируемых данных, а в дальнейшем идет более-менее монотонный рост, т.е. в целом стратегия настроена на обеспечение прибыльной работы. Но это на данных выборки.
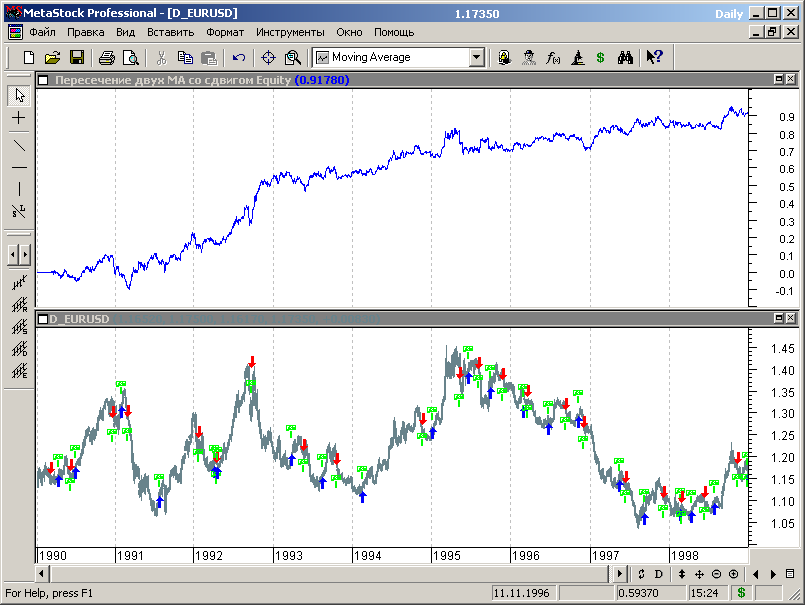
Рис.7.38.
Синим цветом показан график эквити для МТС, полученной на этапе первоначальной оптимизации, красным – для системы, оптимизированной на всем диапазоне исторических данных.
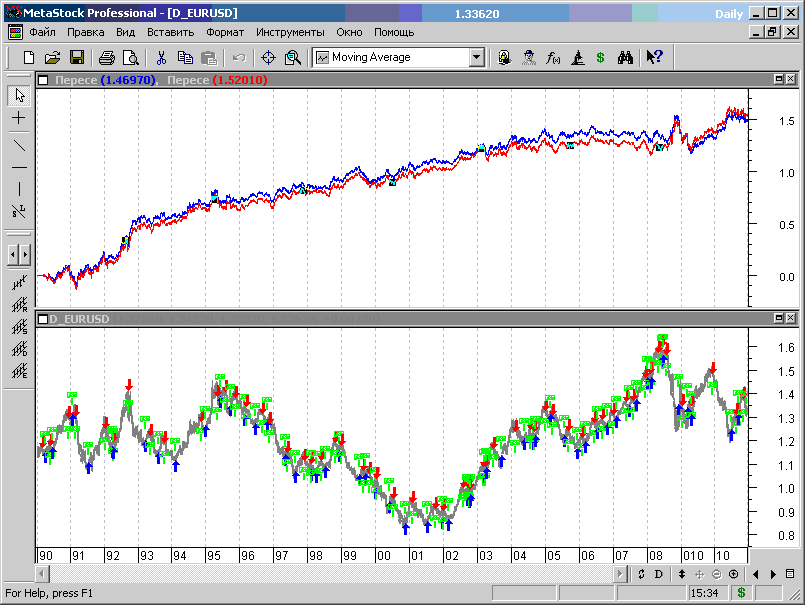
Рис.7.39.
Отличия в поведении линий эквити есть, но они незначительны, т.е. торговая стратегии имеет свойство сохранять свои параметры, полученные в результате оптимизации, с течением времени, что говорит о том, что нам удалось найти некоторую закономерность в изменении рыночных цен, не зависящую от времени и внешних обстоятельств.
В целом стратегия сохраняет свои параметры с течением времени, и хотя наблюдаются участки бесприбыльной и даже убыточной работы, но основная закономерность – это рост профита.
Таким образом, на данных вне выборки МТС тоже проявила себя неплохо, за исключением участка исторических данных, соответствующих заключительной фазе активного развития мирового финансового кризиса 2008 года (рис.7.39) – алгоритм не выдержал чрезмерно высокой волатильности рынков. Однако такого рода потрясений не выдержит ни один алгоритм механизированной торговли на основе индикаторов, ибо кризис, явление единичное, а МТС строятся на основе массовой статистики, полученной в условиях обыденного, повседневного существования рынков. Способ борьбы с такого рода провалами один – антикатастрофические стопы.
7.7.1. Торговая идея.
Этот вариант торговой стратегии рассмотрим по той причине, что он используется в качестве сигнала входа в ряде торговых систем.
Торговая идея незначительно отличается от предыдущего случая. Все отличие заключается в том, что вместо пересечения двух скользящих средних используется пересечение цены и сдвинутой скользящей средней.
Торговые правила для этого случая будут иметь вид:
Buy Order: Cross(C, Mov(ref(C,-opt2),opt1,E))
Sell Order: Cross(Mov(ref(C,-opt2),opt1,E),C)
Sell Short Order: Cross(Mov(ref(C,-opt2),opt1,E),C)
Buy to Cover Order: Cross(C, Mov(ref(C,-opt2),opt1,E))
Сохраняем два параметра оптимизации, как и в предыдущем примере, только немного расширим диапазон изменения переменных по сравнению с результатами п.7.6. Зададим диапазоны переменных оптимизации:
- период скользящей средней, определяемой переменной оптимизации opt1, в диапазоне от 10 до 60 с шагом 1;
- значения переменной оптимизации opt2, определяющей величину сдвига, будем изменять от 5 до 60 с шагом 1.
Привычным движением открываем окно тестера систем, строим новую торговую систему и приступаем к тестированию и первоначальной оптимизации системы.
Первоначальную оптимизацию проводим на стартовом сегменте данных с интервалом от 01.01.1990 до 31.12.1998.
Результаты теста на заданных интервалах изменения переменных оптимизации не показали явных оптимумов по периоду скользящей средней. По сдвигу оптимальное значение находится в более узком интервале значений более 15 и менее 45 (см. рис.7.40).
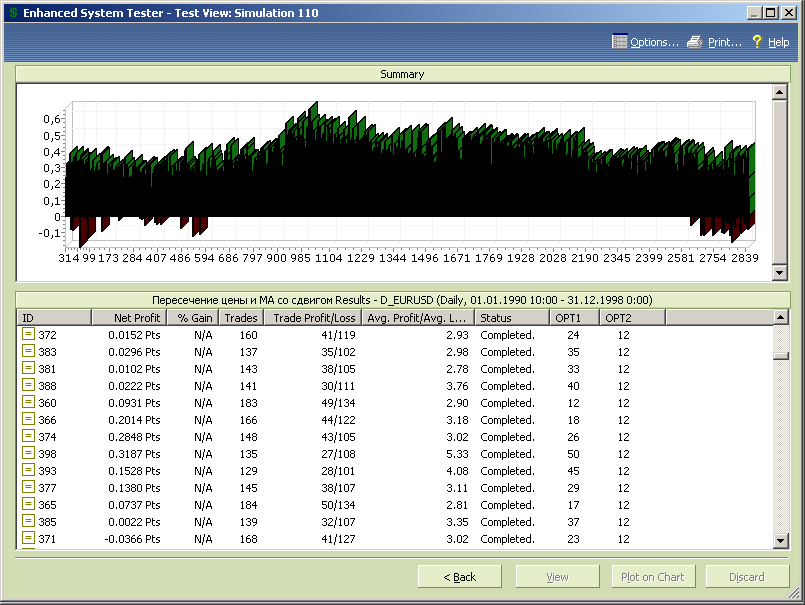
Рис.7.40.
Удаляем данные вне этого интервала из результатов тестирования.
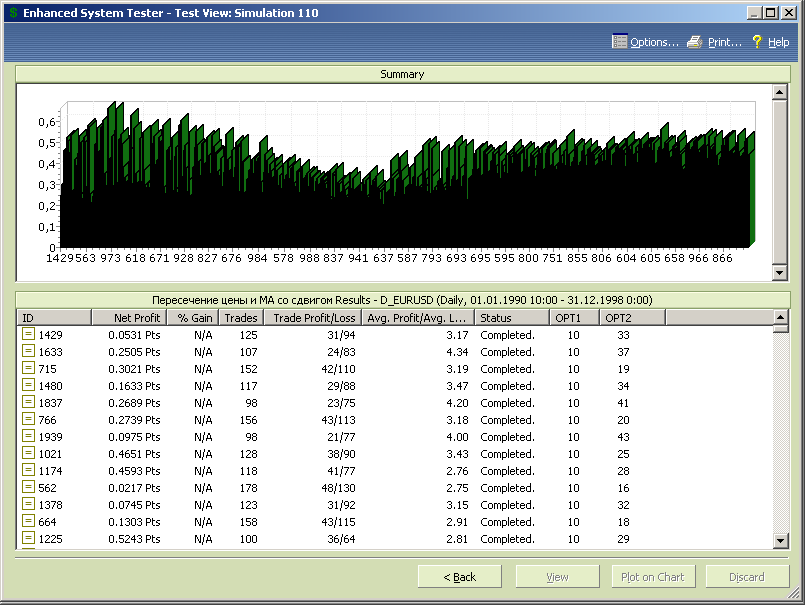
Рис.7.41.
Упорядочивание данных по opt1, как следует из рисунка 7.41, показывает, что оптимальные стратегии находятся в первой трети диапазона и вероятно диапазон необходимо расширить вниз, до меньших значений периода скользящей средней.
Откорректируем диапазон изменения переменной оптимизации opt1, установив его границы от 1 до 25, и проведем повторную оптимизацию МТС.
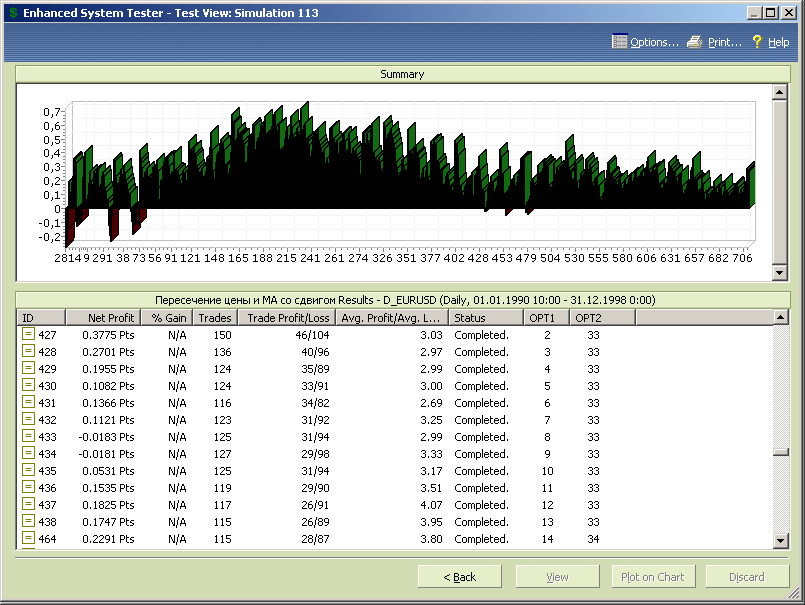
Рис.7.42.
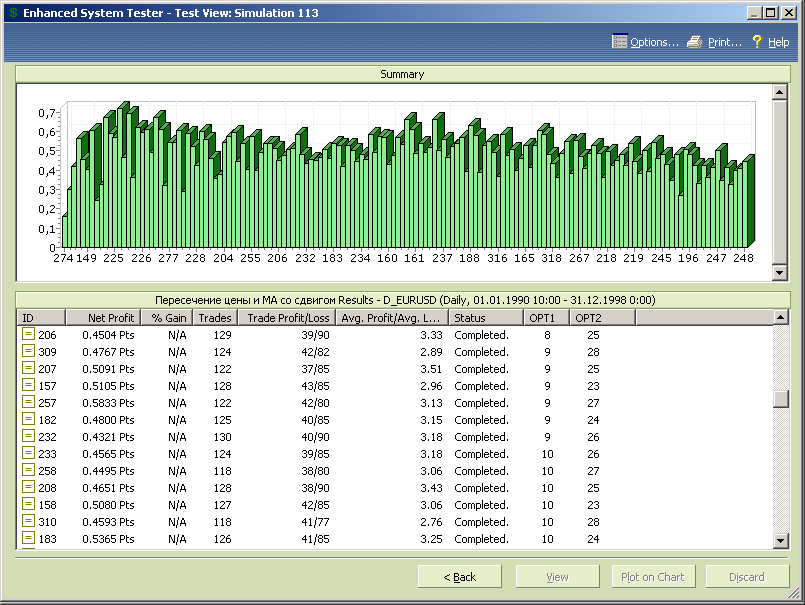
Рис.7.43.
Формируем диапазоны переменных, задавая значения opt1 от 8 до 25 с шагом 1, а opt2 от 23 до 28 с шагом 1 и проводим окончательный тест с формированием эквити.
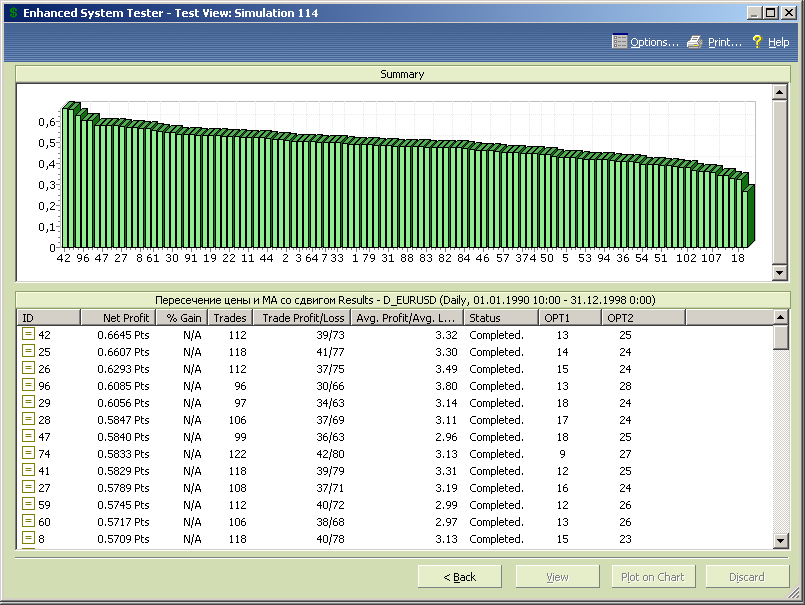
Рис.7.44.
Оптимальные значения переменных, полученные на этапе первоначальной оптимизации, составляют значения 13 для периода скользящей средней и 25 для величины сдвига.
Отметим, что оптимальные значения группируются в окрестности величины сдвига 25, сохраняя преемственность метода относительно стратегии-прототипа, основанной на использовании пересечения скользящей средней и сдвинутой скользящей средней того же периода.
Оптимальная стратегия обеспечивает на интервале тестируемых данных больше 66 фигур профита (6645пп), процент прибыльных сделок 34.8%, но зато отношение средней прибыли к среднему убытку больше трех и составляет величину 3.32. Значение параметра профит-фактор выше 1.78, т.е. выше эмпирически приемлемой границы 1.6, но ненамного.
Объективные параметры стратегии удовлетворительные, но для большей определенности необходимо посмотреть на поведение эквити и проверить МТС на данных «вне выборки».
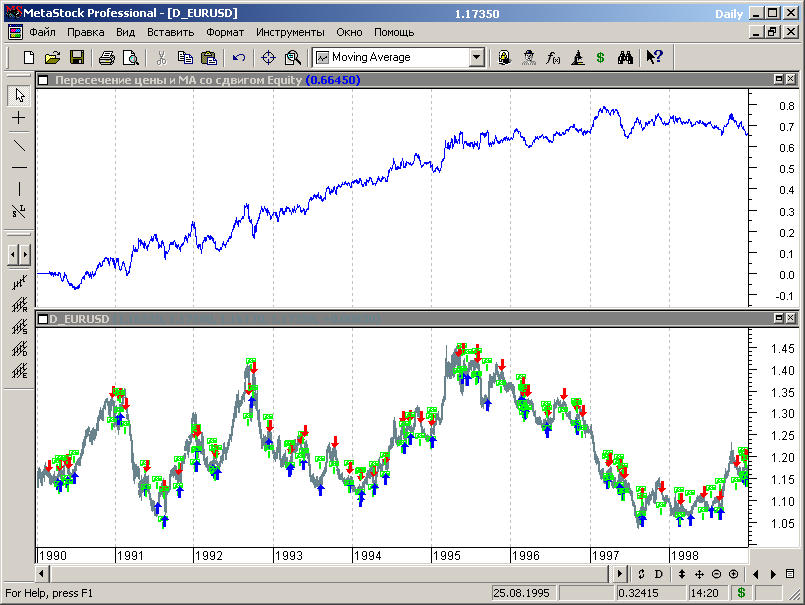
Рис.7.45.
Проведем тестирование стратегии на всем диапазоне исторических данных.
Синим цветом изображен график эквити для МТС, полученной на этапе первоначальной оптимизации, красным – для системы, оптимизированной на всем диапазоне исторических данных.
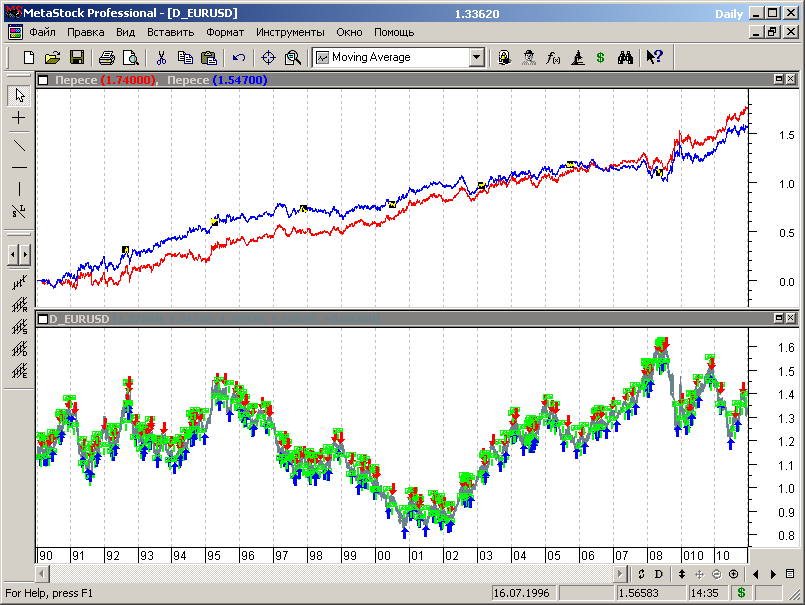
Рис.7.46.
Новые оптимумы стратегии, уточненные по всему диапазону исторических данных, расположены на значениях 8 для периода МА и 23 для величины сдвига.
Отличия в поведении линий эквити стратегии, оптимизированной на всех сегментах данных, и стратегии, оптимизированной на этапе первоначальной оптимизации, конечно же есть. Однако больших отклонений не наблюдается, обе системы приносят прибыль, а МТС и для этого случая сохраняет свои параметры с течением времени.
Следует отметить, что для МТС, основанной на пересечении цены и сдвинутой вперед скользящей средней, последствия финансового кризиса 2008 года не были столь печальны, как для предыдущей из сконструированных нами систем.
Количественные характеристики тестов для обеих систем следующие.
Первоначальная МТС:
- профит - 15470пп;
- процент прибыльных сделок – 30.7%;
- отношение AW/AL – 4.07;
- профит-фактор – 1.80.
МТС, оптимизированная на всех сегментах данных:
- профит - 17400пп;
- процент прибыльных сделок – 36.1%;
- отношение AW/AL – 3.28;
- профит-фактор – 1.85.
Таким образом, и эта МТС на данных «вне выборки» проявила себя неплохо и может служить в качестве прототипа или элемента реальной рабочей стратегии.
7.8.1. Торговая идея.
Эта торговая стратегия эквивалент случаю пересечения цены и скользящей средней, но только сразу для нескольких тайм-фреймов, отличающихся временным масштабом представления данных.
С учетом того факта, что торговая стратегия у нас работает с привязкой графику одного масштаба, разницу масштабов мы учтем масштабированием периодов скользящих средних (рис.7.47).
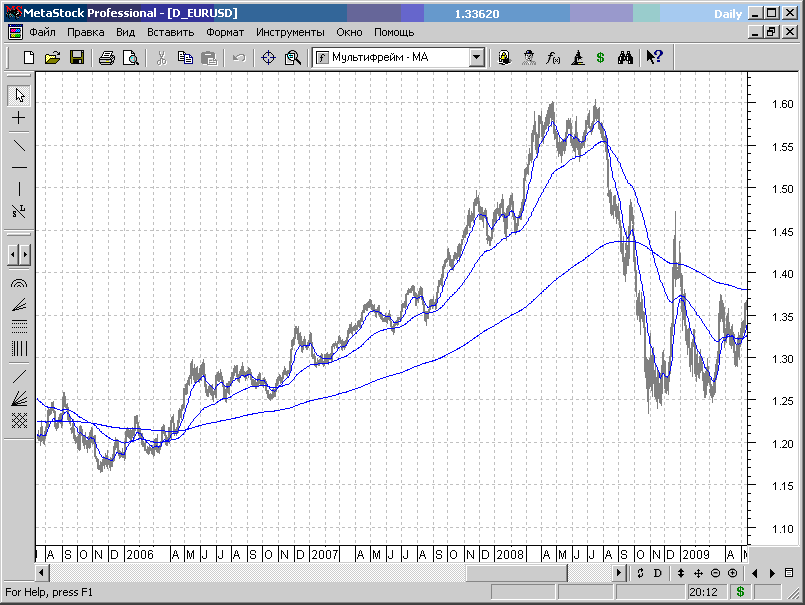
Рис.7.47.
На рис.7.47 представлен график дневного масштаба EURUSD и пользовательским индикатором, представляющим собой три скользящих средних с кратными периодами.
Формула пользовательского индикатора имеет вид:
N1:=Input("Период", 1,50,10);
N2:=Input("Множитель", 2,10,2);
Mov(C,N1,E);
Mov(C,N2*N1,E);
Mov(C,N2*N2*N1,E);
Индикатор формирует на графике три скользящих средних, периоды которых отличаются в N2 раз. (
Суть торговой идеи для этого случая заключается в следующем: мы считаем, что тренд восходящий, если цена больше всех трех скользящих средних, т.е. что три тренда разной длительности на трех кратных тайм-фреймах представления данных классифицируются, как восходящие. Т.е. выполняются все три условия:
C>Mov(C,N1,E);
C>Mov(C,N2*N1,E);
C>Mov(C,N2*N2*N1,E).
Соответственно для нисходящего тренда должны выполняться условия:
C<Mov(C,N1,E);
C<Mov(C,N2*N1,E);
C<Mov(C,N2*N2*N1,E).
Для заданной торговой идеи можно сформировать несколько вариантов торговых систем, отличающихся как формой записи торговых правил, так и нюансами алгоритмов МТС.
Начнем с самого простого.
Торговые правила для простейшего случая симметричной мультифреймовой стратегии будут иметь вид:
Buy Order: (C>Mov(C,opt1,E))*(C>Mov(C,opt2*opt1,E))*(C>Mov(C, opt2*opt2*opt1,E))
Sell Order: (C<Mov(C,opt1,E))*(C<Mov(C,opt2*opt1,E))*(C<Mov(C, opt2*opt2*opt1,E))
Sell Short Order: (C<Mov(C,opt1,E))*(C<Mov(C,opt2*opt1,E))*(C<Mov(C, opt2*opt2*opt1,E))
Buy to Cover Order: (C>Mov(C,opt1,E))*(C>Mov(C,opt2*opt1,E))*(C>Mov(C, opt2*opt2*opt1,E))
Отметим, что по логике работы для задания условия одновременного выполнения всех неравенств в скобках необходимо использовать оператор логического "И" ( оператор AND ), но в целях более сжатой записи торговых правил мы использовали оператор умножения, дающий эквивалентный результат.
Зададим диапазоны изменения переменных для этапа первоначальной оптимизации:
- период самой быстрой скользящей средней, определяемой переменной оптимизации opt1, в диапазоне от 1 до 50 с шагом 1;
- значения переменной оптимизации opt2 будем изменять от 2 до 10 с шагом 0.5.
Открываем окно тестера систем, строим новую торговую систему и приступаем к тестированию и первоначальной оптимизации системы.
Первоначальную оптимизацию проводим на стартовом сегменте данных.
На рисунке 7.48 представлена диаграмма результатов тестов, упорядоченных по переменной opt1.
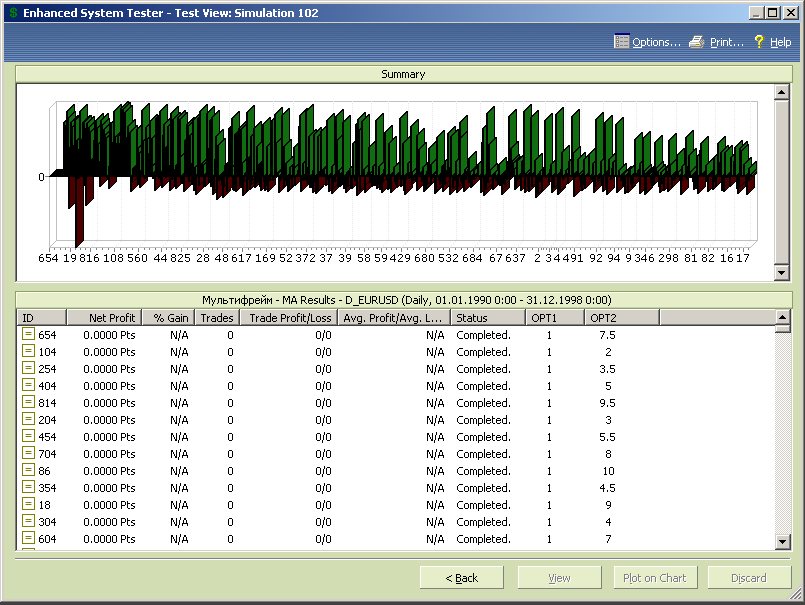
Рис.7.48.
Из представленных данных можно сделать следующие выводы:
- МТС в целом слабо чувствительна к изменению параметра opt1;
- характеристики системы нестабильны, так как в зоне любых значений opt1 диаграмма содержит тесты как с высокой прибылью, так и с убытком, причем эти тесты расположены в непосредственной близости друг от друга.
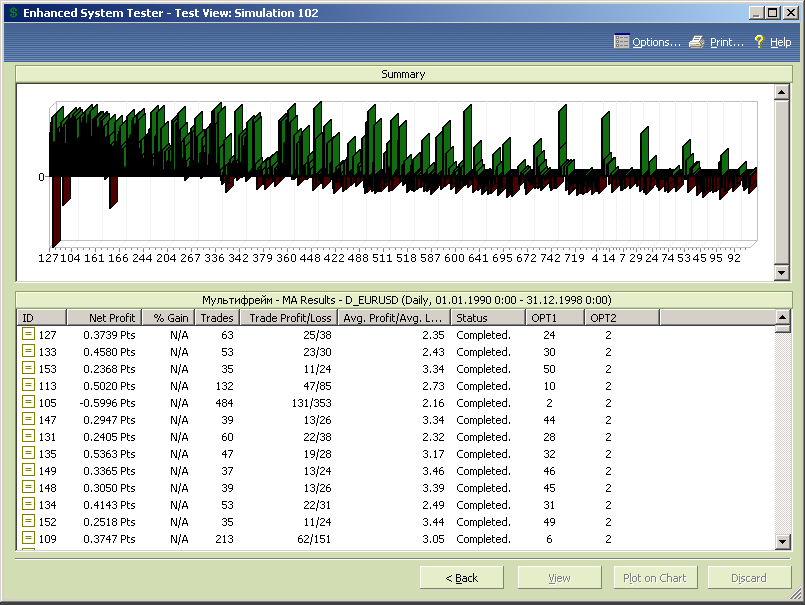
Рис.7.49.
Произведем модификацию торговых правил и изменение диапазонов изменения оптимизационных переменных и продолжим первоначальную оптимизацию.
Торговые правила мы сохраним в прежнем виде:
Buy Order: (C>Mov(C,opt1,E))*(C>Mov(C,opt2*opt1,E))*(C>Mov(C, opt2*opt2*opt1,E))
Sell Order: (C<Mov(C,opt1,E))*(C<Mov(C,opt2*opt1,E))*(C<Mov(C, opt2*opt2*opt1,E))
Sell Short Order: (C<Mov(C,opt1,E))*(C<Mov(C,opt2*opt1,E))*(C<Mov(C, opt2*opt2*opt1,E))
Buy to Cover Order: (C>Mov(C,opt1,E))*(C>Mov(C,opt2*opt1,E))*(C>Mov(C, opt2*opt2*opt1,E))
Основные изменения будут касаться диапазонов оптимизационных переменных.
Прежде всего, отметим, что в предыдущем тесте было множество вариантов с предельно большими значениями периода самой медленной МА. Так, напри значении opt1=50 и opt2=10 период этой МА составлял значение 5000, что явно выходит за пределы разумного. И таких тестов было достаточно много. Поэтому мы переставим акценты и в качестве основной из трех скользящих средних будем использовать скользящую среднюю с самым большим периодом, как определяющую тренд, в направлении которого будет вестись торговля. В этом случае переменная opt2 будет принимать значения меньше единицы.
Зададим диапазон изменения переменной opt1 в пределах от 10 до 100 с шагом 1.
Диапазон изменения переменной opt2, с учетом результатов предыдущего теста, установим от 0.2 до 1.0 с шагом 0.05.
С помощью тестера систем модифицируем диапазоны изменения оптимизационных переменных и проводим новый тест.
Изменяем диапазоны переменных с помощью тестера систем и продолжаем тестирование.
Результаты нового теста, с измененными диапазонами переменных и ограничением максимального МА сверху представлены на рисунке 7.50.
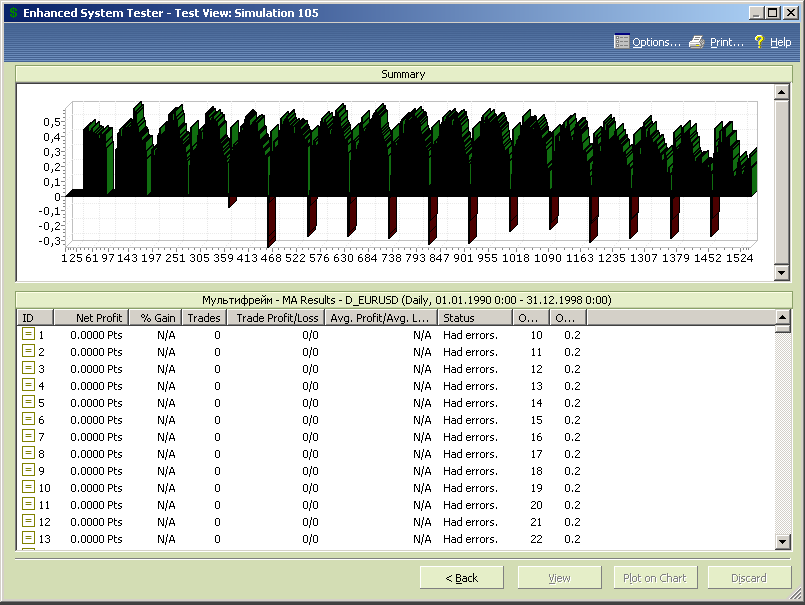
Рис.7.50.
Что же, похоже мы на правильном пути. Однако необходимо разобраться с ошибками теста, которые представлены в таблице рисунка 7.50.
Смотрим. Значение переменной opt1=10, opt2=0.2. Соответственно значение произведения opt1*opt2*opt2 будет равно 0.4, т.е. меньше единицы. А если параметр, определяющий период скользящей средней, принимает значения меньше единицы, то скользящая средняя не вычисляется. Таким образом, ошибочные результаты соответствуют нерабочим комбинациям переменных и мы можем со спокойной совестью удалить их из таблицы перед тем, как проводить дальнейший анализ полученных данных.
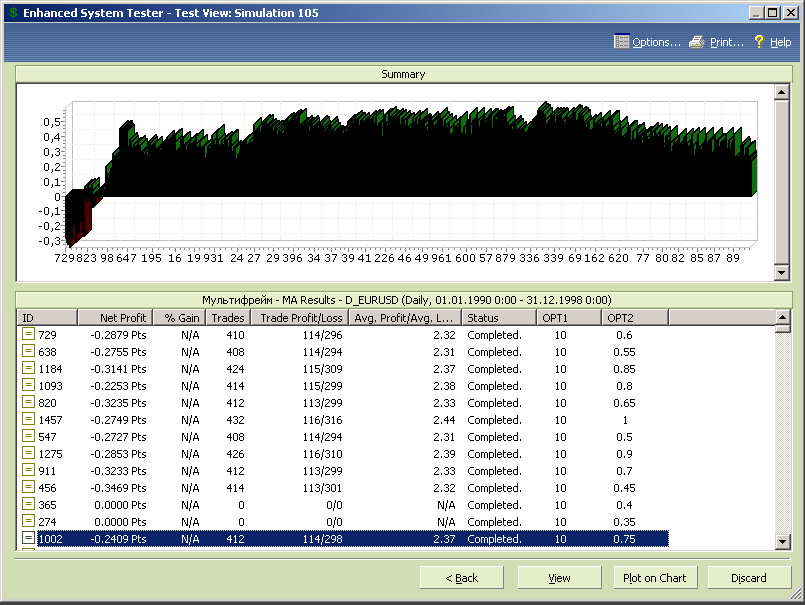
Рис.7.51.
Анализ полученной диаграммы показывает, что только в самом начале диапазона изменения переменной opt1 (при значениях opt1 меньше 18) МТС работает с убытком или приносит незначительную прибыль. Удаляем эти комбинации из теста.
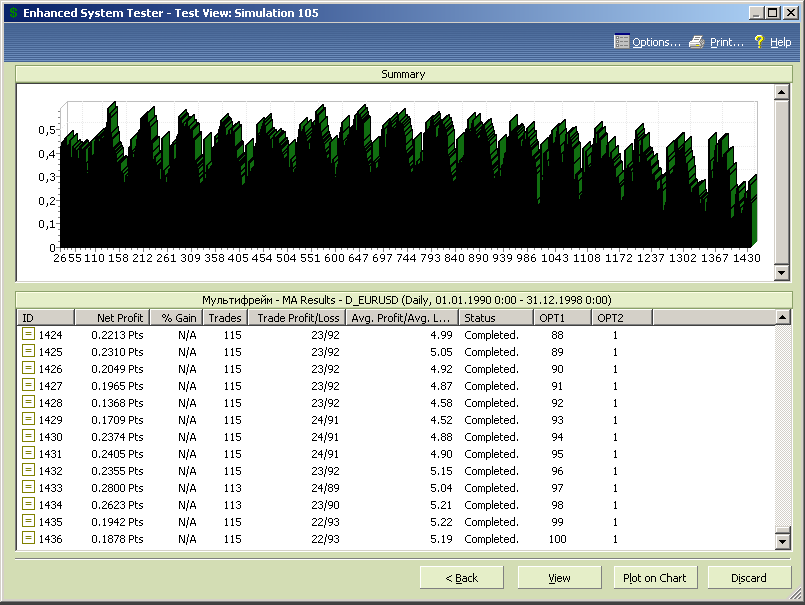
Рис.7.52.
По данным рисунка 7.52 можно сделать вывод, что диапазон значений opt2 от 0.75 и выше можно исключить из рассмотрения в связи с ростом волатильности результатов теста и ростом глубины «провалов» на диаграмме.
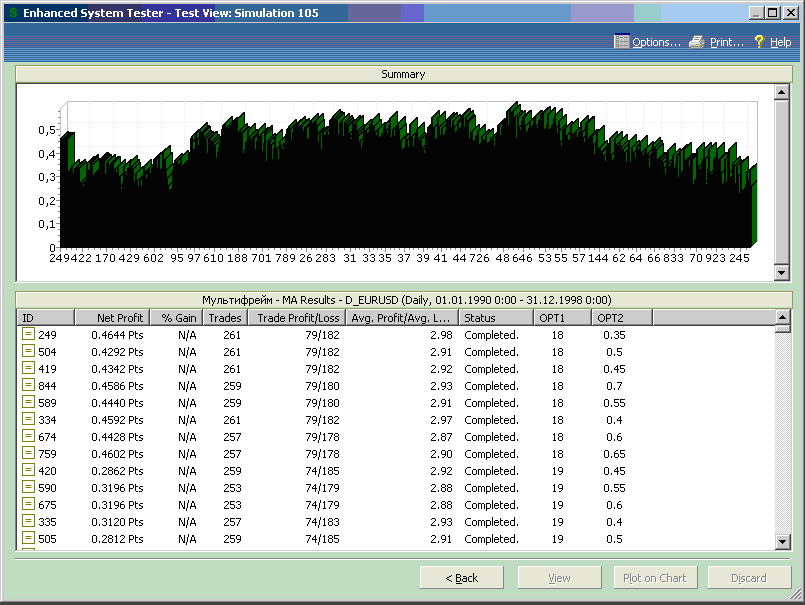
Рис.7.53.
Теперь, когда маскирующий эффект убытков, связанных с неэффективными значениями opt2. исчез, из диаграммы рисунка 7.53 можно видеть, что можно удалить из рассмотрения данные для opt1 больше 85 и меньше 36.
Оставшиеся диапазоны оптимизационных переменных обеспечивают более-менее стабильную работу МТС при любых комбинациях значений opt1 и opt2 (рис.7.54).
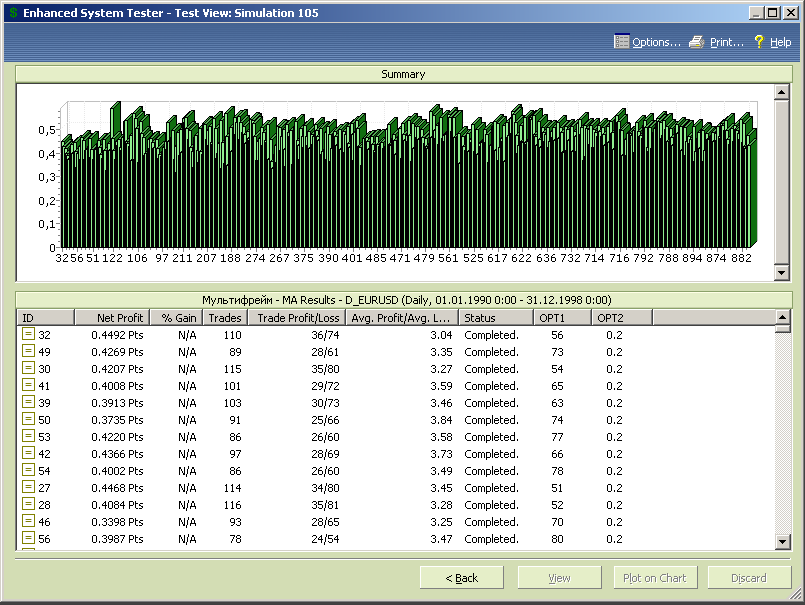
Рис.7.54.
Диаграмма результатов тестирования, упорядоченных по размеру прибыли, представлена на рисунке 7.55.
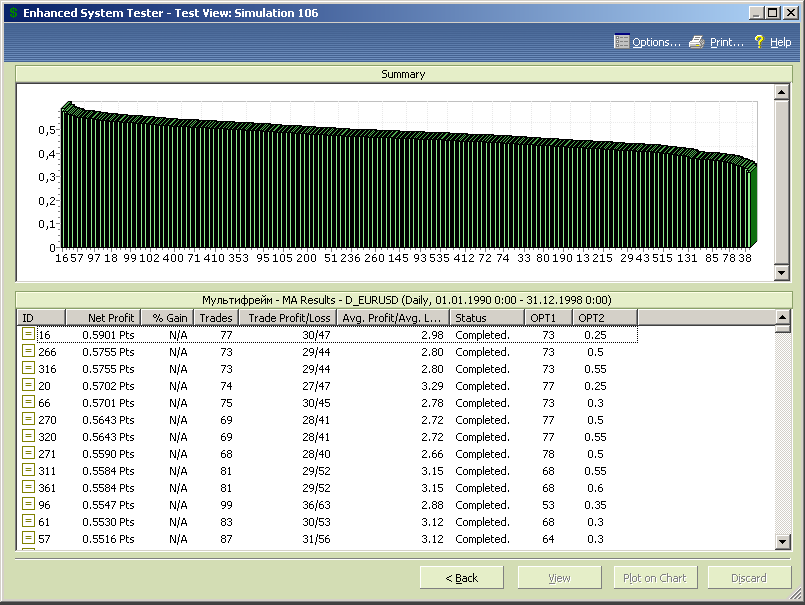
Рис.7.55.
Тест с максимальной прибылью обеспечивает результат +5901пп при значениях параметров оптимизации opt1=73, opt2=0.25.
Система прибыльная, но за что боролись?
Мы усложнили торговые правила, а получили результат хуже, чем для пересечения двух скользящих средних разного периода и для двух скользящих средних одного периода со сдвигом.
Так что данный алгоритм уступает рассмотренным ранее алгоритмам по прибыльности.
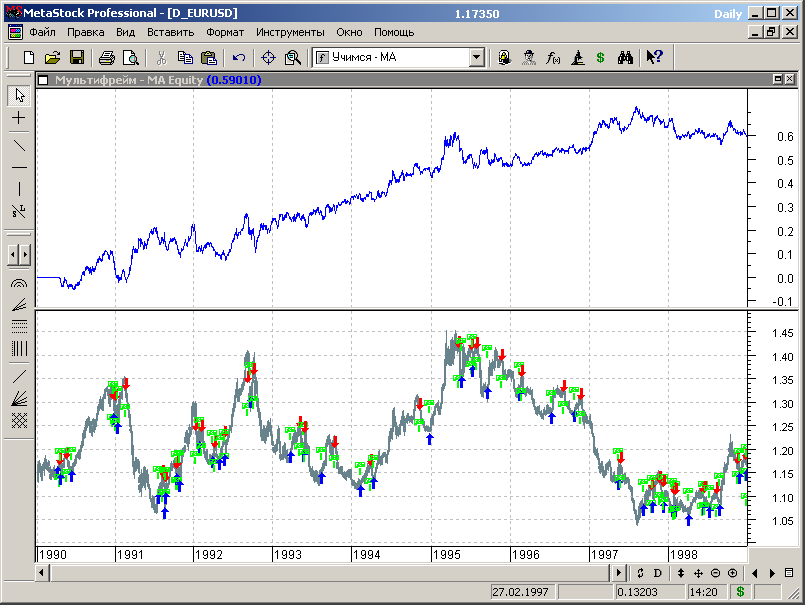
Рис.7.56.
Количественные характеристики теста:
- профит - 5091пп;
- процент прибыльных сделок – 39.0%;
- отношение AW/AL – 2.98;
- профит-фактор – 1.90.
Типовые умеренно хорошие характеристики, но как отмечалось выше, предыдущие более простые стратегии обеспечивали на данных выборки стартового сегмента лучшие параметры. Рассмотрим поведение МТС на данных «вне выборки».
Синим цветом изображен график эквити для МТС, полученной на этапе первоначальной оптимизации, красным – для системы, оптимизированной на всем диапазоне исторических данных.
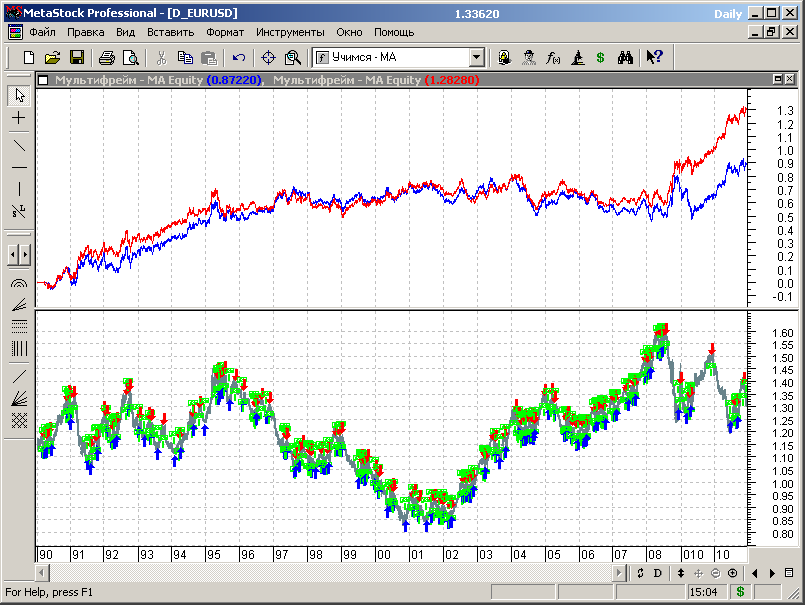
Рис.7.57.
Анализ представленных зависимостей показывает, что рассматриваемая мультифреймовая МТС на основе скользящих средних показала неудовлетворительную работу на данных «вне выборки». Более того, даже оптимизация по всему диапазону исторических данных не улучшила характеристики торговой стратегии на большей части рассматриваемого временного интервала исторических данных. Зарабатывать деньги стратегия начала после середины 2008 года, с началом мирового финансового кризиса (но это тоже на данных выборки).
К существенному недостатку стратегии относится и то, что параметры оптимального теста для всей выборки (opt1=53, opt2=0.6), существенно отличаются от параметров теста на этапе первоначальной оптимизации (opt1=73, opt2=0.25), что говорит о нестабильности параметров МТС.
С учетом полученных результатов мультифреймовая МТС в рассмотренном варианте ее построения вряд ли может быть рекомендована для использования в практической торговле.
7.9.1. Торговая идея.
Попробуем модифицировать предыдущую торговую стратегию следующим образом.
Сохраним наиболее медленную скользящую среднюю, как указатель тренда, а две более быстрых будем использовать для открытия и закрытия позиций следующим образом (рис.7.58):
- если цена закрытия больше самой медленной скользящей средней, то будем открывать только длинные позиции;
- если цена закрытия меньше самой медленной скользящей средней, то будем открывать только короткие позиции;
- сигналом для входа в рынок, при соблюдении одного из первых двух условий, является пересечение двух более быстрых скользящих средних;
- сигналом для закрытия позиций является пересечение двух более быстрых скользящих средних в противоположном направлении, независимо от расположения медленной скользящей средней относительно цены закрытия.
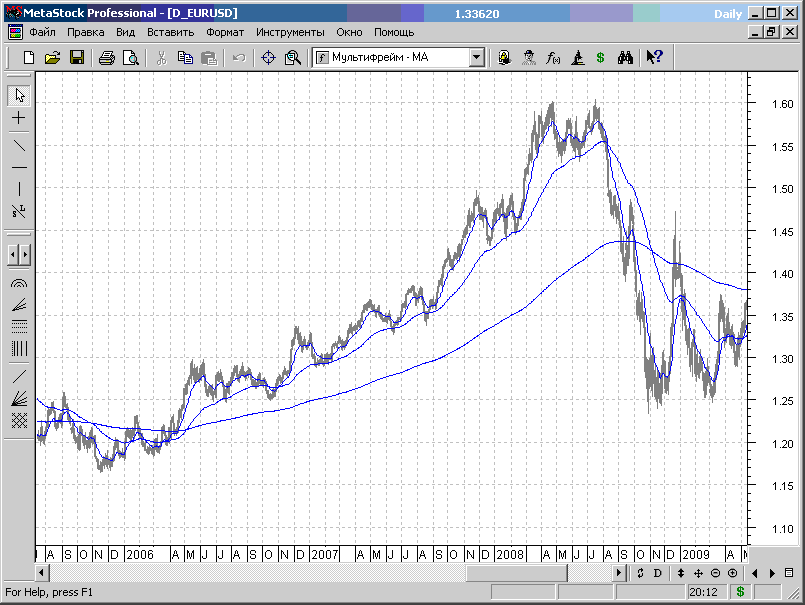
Рис.7.58.
Торговые правила будут иметь вид:
Buy Order: (C>Mov(C,opt1,E))*Cross(Mov(C,opt2*opt2*opt1,E),Mo v(C, opt2*opt1,E))
Sell Order: Cross(Mov(C,opt2*opt1,E),Mov(C, opt2*opt2*opt1,E))
Sell Short Order: (C<Mov(C,opt1,E))*Cross(Mov(C,opt2*opt1,E),Mov(C, opt2*opt2*opt1,E))
Buy to Cover Order: Cross(Mov(C,opt2*opt2*opt1,E),Mov(C, opt2*opt1,E))
Зададим диапазоны изменения переменных для этапа первоначальной оптимизации:
- диапазон переменной оптимизации opt1 от 10 до 100 с шагом 1;
- значения переменной оптимизации opt2 будем изменять от 0.2 до 0.8 с шагом 0.05.
Открываем окно тестера систем, строим новую торговую систему и приступаем к тестированию и первоначальной оптимизации системы.
Результаты тестирования на данных «вне выборки», упорядоченные по росту прибыльности системы, представлены на рисунке 7.61.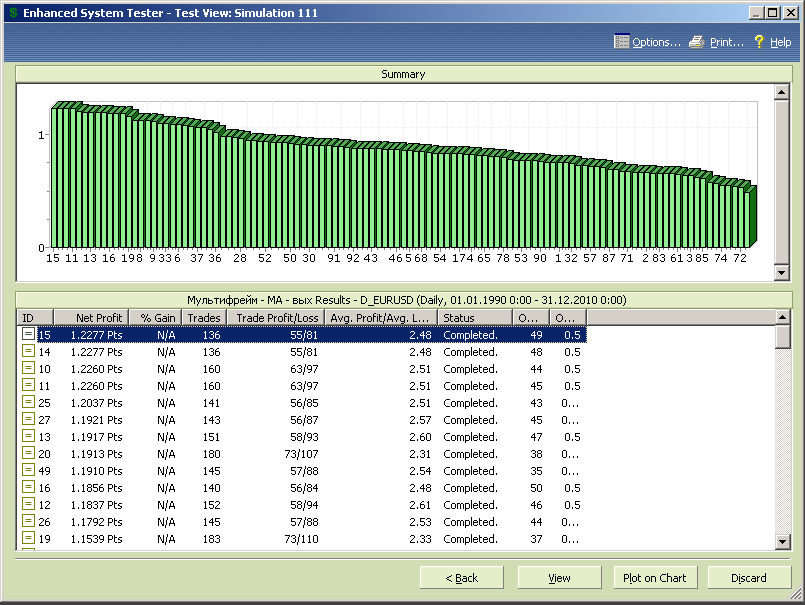
Рис.7.61.
Параметры первоначальной МТС(opt1=47, opt2=0.7) и системы, оптимизированной на всем интервале данных (opt1=49, opt2=0.5), также значительно отличаются, как и в предыдущем примере, но уже только по второму параметру, влияние которого на прибыльность стратегии меньше, чем влияние первого.
Графики эквити для всего диапазона данных, включающего интервал «вне выборки», представлены на рисунке 7.62. Синим цветом изображен график эквити для МТС, полученной на этапе первоначальной оптимизации, красным – для системы, оптимизированной на всем диапазоне исторических данных.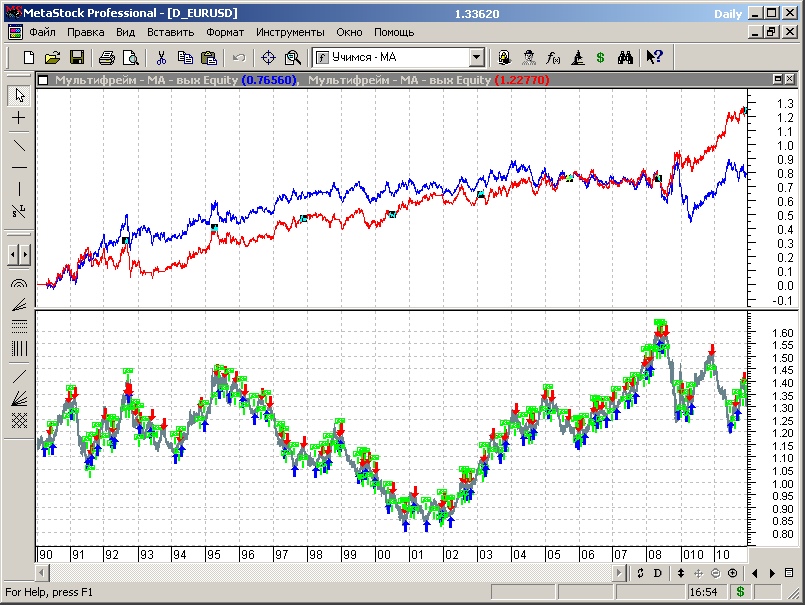
Рис.7.62.
Анализ представленных зависимостей показывает, что и эта версия МТС далека от идеальной и вряд ли будет пригодна для реальной работы в чистом виде, поскольку на данных «вне выборки» результат теста не может считаться удовлетворительным.
7.10. Торговые системы на основе индикатора аллигатор Б.Вильямса
7.10.1. Индикатор «Аллигатор» Б.Вильмса.
Мнения о книгах Б.Вильямса «Торговый Хаос» и «Новые измерения в биржевой торговле» в трейдерской среде занимают диапазон от полного неприятия до восторженного почитания. Чего нет, так это равнодушия, а раз о книгах и методе говорят, то что-то в них есть, по крайней мере следует отдать должное популяризаторскому таланту Б.Вильямса.
Отметим, что торговая стратегия Б.Вильямса – это не механическая торговая система, а некий торгово-аналитический комплекс из большого набора правил и приемов анализа рынка и совершения торговых операций, руководствуясь которым каждый может создать для себя свою торговую стратегию.
В настоящем подразделе мы рассмотрим один из элементов, входящий в торгово-аналитический комплекс Б.Вильямса и основанный на применении набора сдвинутых скользящих средних, т.н. «аллигатор» Б.Вильямса, и простейшие торговые стратегии, которые можно построить на основе этого индикатора.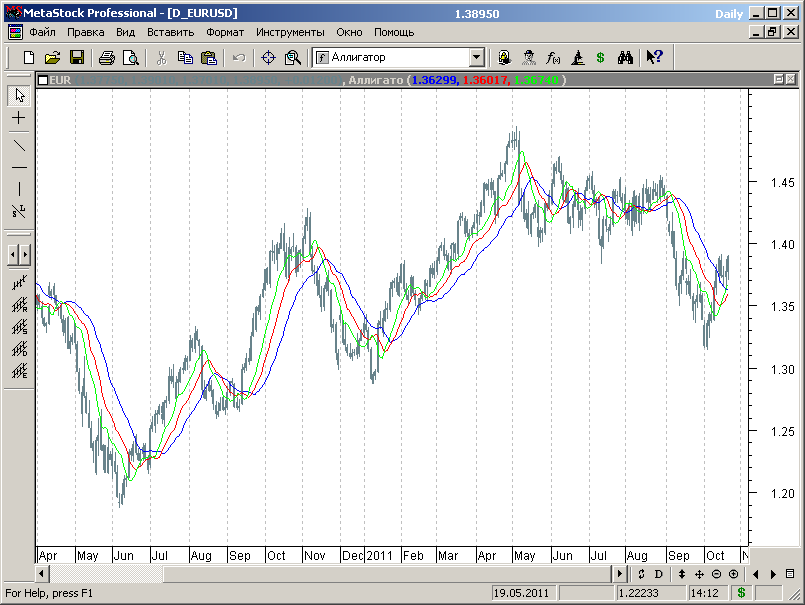
Рис.7.63.
Индикатор аллигатор (см. рис.7.63) представляет собой три сдвинутых скользящих средних различного периода с разным сдвигом, рассматриваемых в совокупности, как один объект.
Существуют две версии аллигатора, на простых и на экспоненциальных скользящих средних. Обе версии практически эквивалентны, мы будем рассматривать версию на экспоненциальных скользящих средних.
Формулы для пользовательского индикатора «аллигатор» на основе экспоненциальных средних в Метасток будут иметь вид:
Mov(Ref((H+L)/2,-8),25,E); {аллигатор – синяя линия}
Mov(Ref((H+L)/2,-5),15,E); {аллигатор – красная линия}
Mov(Ref((H+L)/2,-3),9,E); {аллигатор – зеленая линия}
Таким образом, аллигатор представляет собой не что иное, как набор из трех сдвинутых скользящих средних с периодами 9 (сдвиг 3), 15 (сдвиг 5) и 25 (сдвиг 8), вычисляемых на медианной цене графика.
На графике линии раскрашиваются разными цветами, а именно:
- самая быстрая скользящая средняя с периодом 9 изображается линией зеленого цвета и называется губами аллигатора;
- линия с периодом 15 красная и называется зубами аллигатора;
- и наконец, самая медленная из трех скользящая средняя с периодом 25, изображаемая синим цветом, символизирует собой челюсти аллигатора.
Различные комбинации взаимного расположения графика цены и элементов индикатора служат руководством к тем или иным действиям на рынке.
Аллигатор очень популярен, особенно среди начинающих трейдеров. Рассмотрим на тестах, что дает применение аллигатора в качестве элемента торговой стратегии.
7.10.2. Торговая идея.
Б.Вильямс, психолог по образованию, пишет образно и ярко, учитывая психологию восприятия текста читателем. Поэтому его книги запоминаются, особенно если они были прочитаны на этапе начального знакомства с рынком.
Аллигатор, по словам Б.Вильямса, охотится за добычей, которой является цена.
Когда линии аллигатора переплетены с линией графика цены, то добыча поймана, аллигатор сыт и пассивен. Трейдер в этот момент тоже находится в режиме ожидания.
Пользуясь пассивностью аллигатора добыча – цена начинает потихоньку ускользать из зоны линий индикатора, аллигатор начинает чувствовать голод, просыпается и открывает пасть, пытаясь поймать ускользающую добычу. Вначале размыкаются губы аллигатора – зеленая линия, затем зубы – красная, и наконец распахиваются челюсти – синяя линия.
Линии индикатора выстраиваются в порядке зеленая-красная-синяя и движутся вслед за ценой, пока продолжается тренд. Поскольку тренд не может длиться бесконечно, то рано или поздно аллигатор настигает добычу и цена опять попадает в зону линий индикатора. Процесс, с теми или иными отличиями циклически повторяется по мере появления и развития новых трендов.
Первая торговая идея, которая возникает при рассмотрении индикатора аллигатор Б.Вильямса – это использовать аллигатор в качестве индикатора тренда. Если линии индикатора вытраиваются в порядке зеленая-красная-синяя, то очевидно, что тренд восходящий, если порядок линий синяя-красная-зеленая, то тренд нисходящий (рис.7.63).
Попробуем протестировать торговую стратегию, основанную на порядке расположения линий аллигатора.
7.10.3. Торговые правила -1.
Торговые правила для этого случая будут иметь вид:
Buy Order: (Mov(Ref((H+L)/2,-3),9,E) > Mov(Ref((H+L)/2,-5),15,E))*
(Mov(Ref((H+L)/2,-5),15,E) > Mov(Ref((H+L)/2,-8),25,E))
Sell Order: (Mov(Ref((H+L)/2,-3),9,E) < Mov(Ref((H+L)/2,-5),15,E))*
(Mov(Ref((H+L)/2,-5),15,E) < Mov(Ref((H+L)/2,-8),25,E))
Sell Short Order: (Mov(Ref((H+L)/2,-3),9,E) < Mov(Ref((H+L)/2,-5),15,E))*
(Mov(Ref((H+L)/2,-5),15,E) < Mov(Ref((H+L)/2,-8),25,E))
Buy to Cover Order: (Mov(Ref((H+L)/2,-3),9,E) > Mov(Ref((H+L)/2,-5),15,E))*
(Mov(Ref((H+L)/2,-5),15,E) > Mov(Ref((H+L)/2,-8),25,E))
Для покупок мы выделили одновременное выполнение условий, что зеленая линия больше красной, а красная больше синей.
Для продаж – одновременное выполнение условий, что зеленая линия меньше красной, а красная меньше синей.
Оптимизацию использовать не будем, проверим аллигатор в первозданном виде.
Поскольку параметры стратегии не меняются, то нет необходимости производить сегментирование данных и циклическую оптимизацию, стратегию сразу можно проверять на всем интервале исторических данных.
7.10.4. Результаты тестирования.
Открываем окно тестера систем, строим новую торговую систему «Аллигатор» и приступаем к ее тестированию.
Эквити для результатов теста на протяженности интервала, включающего все сегменты исторических данных, представлена на рисунке 7.64.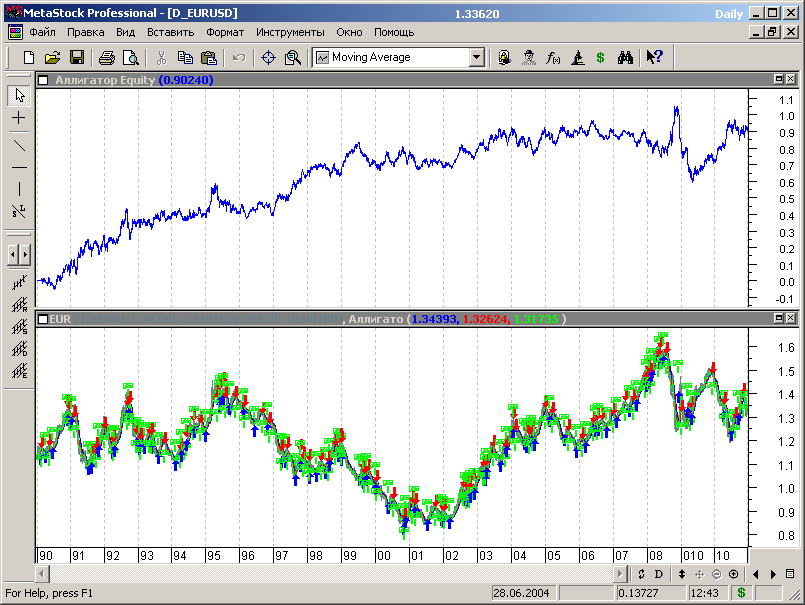
Рис.7.64.
Сразу отметим, что прибыльность стратегии несколько ниже, чем для МТС, рассмотренных нами ранее, но ведь здесь мы не использовали оптимизацию. И еще один момент - в период до публикаций книг Б.Вильмча (конец 90-х) стратегия работала лучше, чем после публикации, т.е. рынок или изменился и перестал соответствовать методу, или приспособился к системе Б.Вильямса.
Проанализируем причины убыточности МТС на примере провала эквити в конце 2008 года (рис.7.65).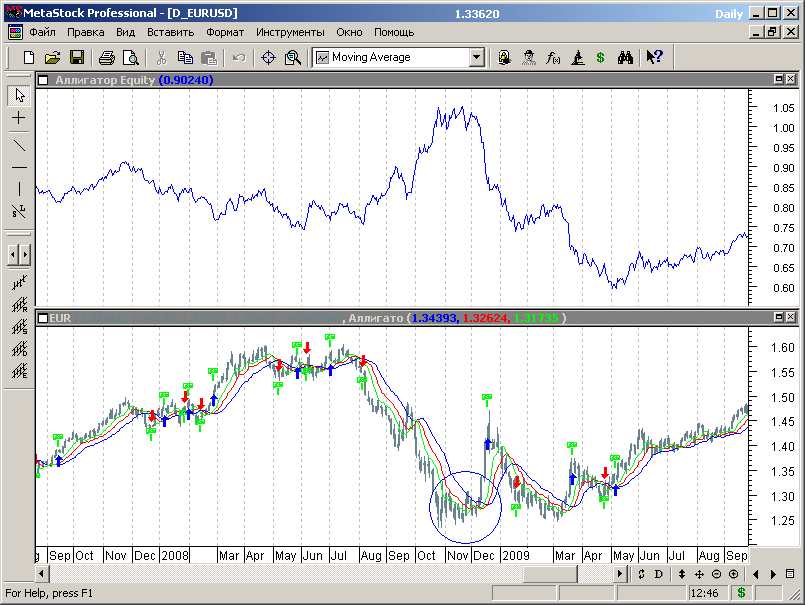
Рис.7.65.
Из рисунка 7.65 можно видеть, что МТС четко отследила в середине 2008 года начало нисходящего тренда, вызванного мировым финансовым кризисом, но из-за запаздывания аллигатора не справилась с коррекцией в конце 2008 года, с опозданием закрыв продажи и совершив покупку на пике рынка перед новым циклом падения котировок.
Вспомним, что в своих книгах Б.Вильямс рекомендует выходить из рынка не дожидаясь разворота тренда в случае, если цена закрытия пресекает красную линию аллигатора. Модифицируем торговую идею, добавив это условие в торговые правила стратегии, и посмотрим на поведение МТС.
7.10.5. Торговые правила -1.
Модифицированные торговые запишутся в виде:
Buy Order: (C> Mov(Ref((H+L)/2,-5),15,E))*
(Mov(Ref((H+L)/2,-3),9,E) > Mov(Ref((H+L)/2,-5),15,E))*
(Mov(Ref((H+L)/2,-5),15,E) > Mov(Ref((H+L)/2,-8),25,E))
Sell Order: (C< Mov(Ref((H+L)/2,-5),15,E)) OR
(Mov(Ref((H+L)/2,-3),9,E) < Mov(Ref((H+L)/2,-5),15,E))*
(Mov(Ref((H+L)/2,-5),15,E) < Mov(Ref((H+L)/2,-8),25,E))
Sell Short Order: (C< Mov(Ref((H+L)/2,-5),15,E))*
(Mov(Ref((H+L)/2,-3),9,E) < Mov(Ref((H+L)/2,-5),15,E))*
(Mov(Ref((H+L)/2,-5),15,E) < Mov(Ref((H+L)/2,-8),25,E))
Buy to Cover Order: (C> Mov(Ref((H+L)/2,-5),15,E)) OR
(Mov(Ref((H+L)/2,-3),9,E) > Mov(Ref((H+L)/2,-5),15,E))*
(Mov(Ref((H+L)/2,-5),15,E) > Mov(Ref((H+L)/2,-8),25,E))
Условие для открытия позиций мы дополнили проверкой взаимного расположения цены закрытия и кратной линии аллигатора, чтобы не возникло конфликта между правилами открытия и закрытия позиций.
Закрытие позиции производится либо по условию взаимного расположения линий аллигатора либо по пересечению ценой закрытия красной линии.
Приступаем к тестированию.
7.10.6. Результаты тестирования -1.
М-да... Как показывает график эквити, представленный на рисунке 7.66, нововведение не улучшило параметры стратегии.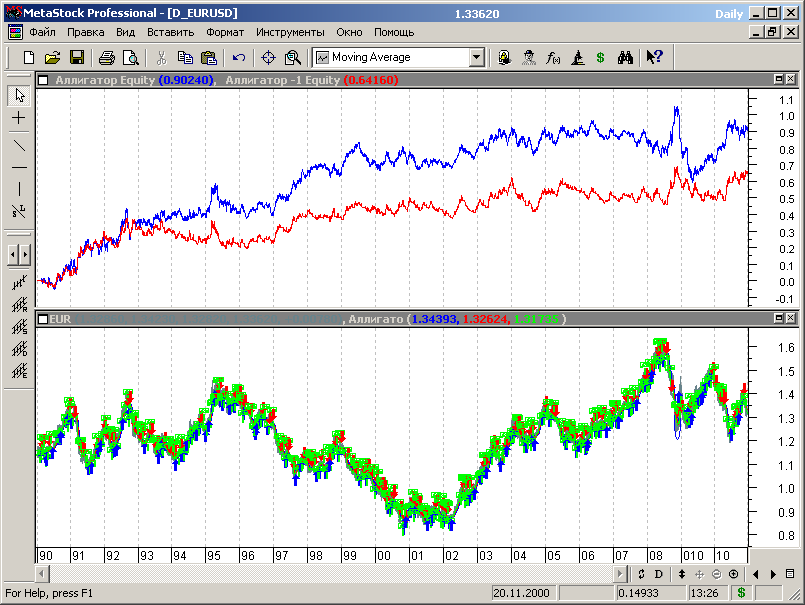
Рис. 7.66.
Синим цветом представлена эквити для исходной МТС, красным – с добавлением выхода по пересечению ценой закрытия красной линии.
Провалы в кризисных ситуациях уменьшились, но уменьшилась и без того невысокая прибыльность системы.
В общем, двигаться в этом направлении, пожалуй, не стоит.
7.10.7. Модификация торговой идеи.
Вернемся еще раз к методике Б.Вильямса.
Как уже упоминалось, запрограммировать все сигналы и признаки, используемые в его торгово-аналитическом комплексе практически невозможно, так как всегда присутствуют признаки для открытия позиций во взаимно-исключающих направлениях, и выбор направления торговли зависит от трейдера, его опыта и его трактовки ситуации.
Но и наша МТС – это достаточно вольная трактовка одного из способов применения индикатора аллигатор, основанная на изучении графика цены и индикатора.
Б.Вильямс не настаивает на упорядоченном расположении линий индикатора. В одном из его подходов говорится, что открывать позицию на покупку нужно, когда цена ушла из зоны переплетения линий аллигатора вверх и пробила предыдущий локальный максимум (см. рис.7.67, точка покупок отмечена стрелкой).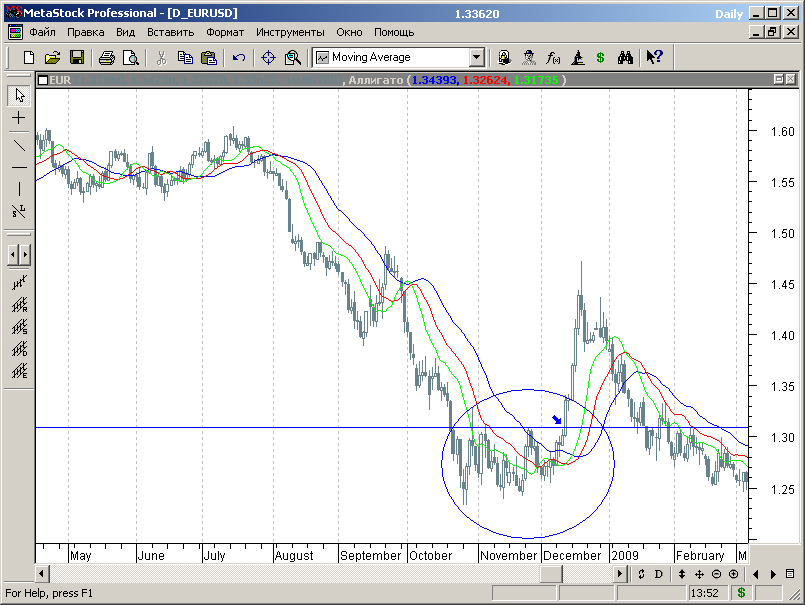
Рис.7.67.
Соответственно, позиция на продажу открывается, когда цена ушла из зоны переплетения линий аллигатора вниз и пробила предыдущий локальный минимум.
Т.е. в этом случае реализуется типичная пробойная стратегия следования за трендом.
Чтобы запрограммировать такой алгоритм, нам необходим индикатор, который выделяет локальные максимумы и минимумы рынка.
В программном комплексе Метасток есть возможность построить такие индикаторы с помощью встроенных функций 1.68 Peak Value (Пиковое значение):
и 1.98 Trough (Донышко):
Пример графика с пользовательским индикатором, выделяющими уровень последнего локального максимума или минимума с помощью функций «Peak Value» и «Trough», представлен на рисунке 7.68.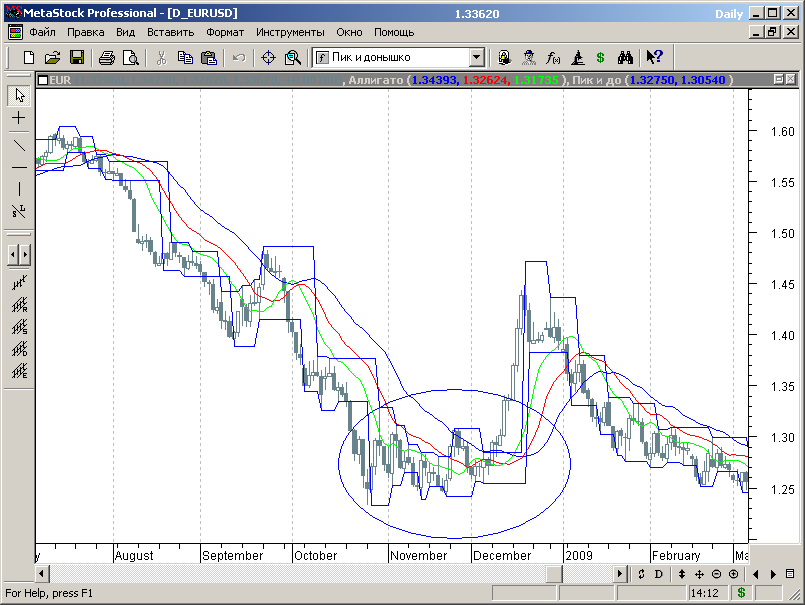
Рис.7.68.
Осталось внести изменения в торговые правила и можно приступать к тестированию.
7.10.8. Торговые правила - 3.
Условие, что цена закрытия больше или меньше линий аллигатора, записывается попарным сравнением цены с каждой из линий, а превышение ценой пика или донышка с помощью функций Cross (см. справочный раздел).
Выход из позиции будем осуществлять по условию открытия позиции противоположного направления, либо по пересечению цены закрытия и красной линии аллигатора в соответствии с рекомендациями Б.Вильямса.
Торговые правила, реализующие эти условия, будут иметь вид:
Buy Order: Cross(C, peak(1,H,0.2))*(C > Mov(Ref((H+L)/2,-3),9,E))*(C > Mov(Ref((H+L)/2,-5),15,E))*(C > Mov(Ref((H+L)/2,-8),25,E))
Sell Order: (C< Mov(Ref((H+L)/2,-5),15,E)) OR Cross(Trough(1,L,0.2),C)*(C < Mov(Ref((H+L)/2,-3),9,E))*(C < Mov(Ref((H+L)/2,-5),15,E))*(C < Mov(Ref((H+L)/2,-8),25,E))
Sell Short Order: Cross(Trough(1,L,0.2),C)*(C < Mov(Ref((H+L)/2,-3),9,E))*(C < Mov(Ref((H+L)/2,-5),15,E))*(C < Mov(Ref((H+L)/2,-8),25,E))
Buy to Cover Order: (C> Mov(Ref((H+L)/2,-5),15,E)) OR Cross(C, peak(1,H,0.2))*(C > Mov(Ref((H+L)/2,-3),9,E))*(C > Mov(Ref((H+L)/2,-5),15,E))*(C > Mov(Ref((H+L)/2,-8),25,E))
Открываем тестер, строим новую систему и проводим тест.
Результаты тестирования представлены на графиках рисунка 7.69.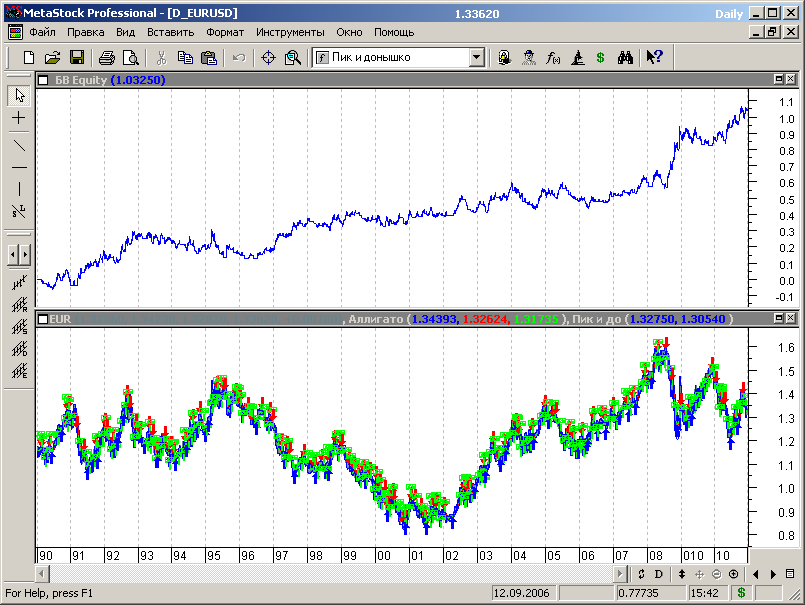
Рис.7.69.
К положительным качествам тестируемой стратегии, по сравнению с предыдущими МТС, которые также использовали индикатор аллигатор, следует отнести более высокий уровень прибыли (полученный, кстати, без оптимизации) и отсутствие катастрофических провалов на любых участках рынка.
К недостаткам стратегии следует отнести наличие затяжных периодов бесприбыльной и убыточной работы, хотя и не катастрофического характера.
Можно ли улучшить характеристики этой стратегии модификацией существующих и/или введением дополнительных правил совершения торговых операций, описанных в книгах Б.Вильмса?
Вполне возможно, и если вас интересуют торговые методы, описанные в книгах «Торговый хаос» или «Новые измерения в биржевой торговле», то, используя аппарат Метасток, вы можете проверить предполагаемые к использованию вами алгоритмы торговли на исторических данных и будете точно представлять возможности этих торговых методов для работы на рынке.
На графике рисунка 7.70 в увеличенном масштабе представлены данные для интервала времени, соответствующего началу активной фазы мирового финансового кризиса в июле-августе 2008 года и далее.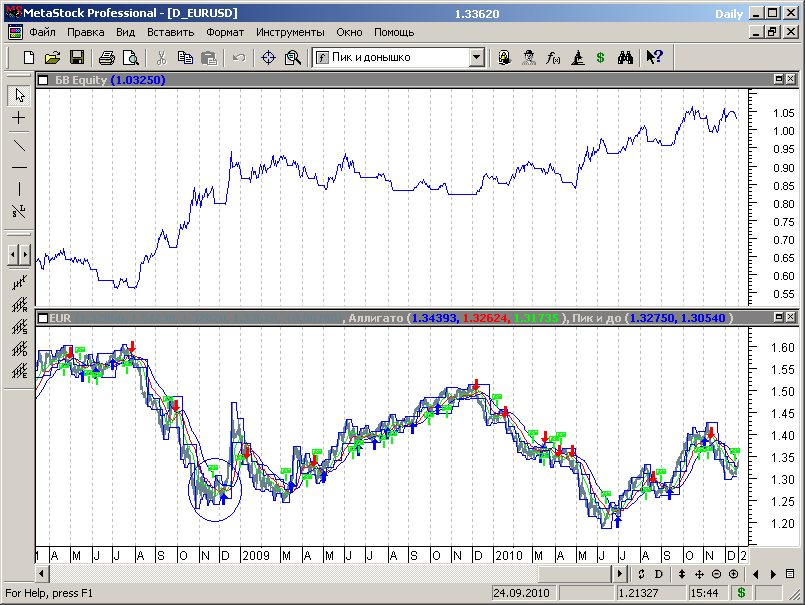
Рис.7.70.
Из представленных данных видно, что тестируемая торговая стратегия успешно вошла в рынок в начале и отследила падение котировок в начале кризиса, с прибылью отработала быстрые коррекции и более-менее успешно справилась с задачами обеспечения прибыльной торговли в дальнейшем, не допуская значительных провалов эквити и обеспечивая циклический рост прибыли.
К несомненным плюсам МТС относится то, что она ограничивает убыток не давая ему вырасти и выходя из рынка по «красной линии» аллигатора.
Так что потенциал у аллигатора и прочих приемов Б.Вильямса несомненно есть, что и показали результаты тестирования, хотя в целом, по критерию размера полученной прибыли, этот подход в рассмотренных вариантах не дает результатов лучше, чем простое пересечение двух скользящих средних.
7.11. Оптимизация торговых систем на основе аллигатора.
7.11.1. Аллигатор с оптимизацией – торговые правила
Проведем оптимизацию МТС на основе аллигатора, изменяя периоды и сдвиг скользящих средних и сохраняя (с точностью до целого числа) соотношение между периодами скользящих средних и сдвигом. Торговые правила для этого случая будут иметь вид:
Buy Order: (Mov(Ref((H+L)/2,-3*opt1),9*opt1,E) > Mov(Ref((H+L)/2,-5*opt1),15*opt1,E))*
(Mov(Ref((H+L)/2,-5*opt1),15*opt1,E) > Mov(Ref((H+L)/2,-8*opt1),25*opt1,E))
Sell Order: (Mov(Ref((H+L)/2,-3*opt1),9*opt1,E) < Mov(Ref((H+L)/2,-5*opt1),15*opt1,E))*
(Mov(Ref((H+L)/2,-5*opt1),15*opt1,E) < Mov(Ref((H+L)/2,-8*opt1),25*opt1,E))
Sell Short Order: (Mov(Ref((H+L)/2,-3*opt1),9*opt1,E) < Mov(Ref((H+L)/2,-5*opt1),15*opt1,E))*
(Mov(Ref((H+L)/2,-5*opt1),15*opt1,E) < Mov(Ref((H+L)/2,-8*opt1),25*opt1,E))
Buy to Cover Order: (Mov(Ref((H+L)/2,-3*opt1),9*opt1,E) > Mov(Ref((H+L)/2,-5*opt1),15*opt1,E))*
(Mov(Ref((H+L)/2,-5*opt1),15*opt1,E) > Mov(Ref((H+L)/2,-8*opt1),25*opt1,E))
Диапазон оптимизационной переменной зададим от 0.5 до 5 с шагом 0.05.
Проведем первоначальную оптимизацию на стартовом сегменте данных.
Оптимизация в пределах стартового сегмента данных показывает оптимум на значении параметра оптимизации opt1=1 (рис.7.71).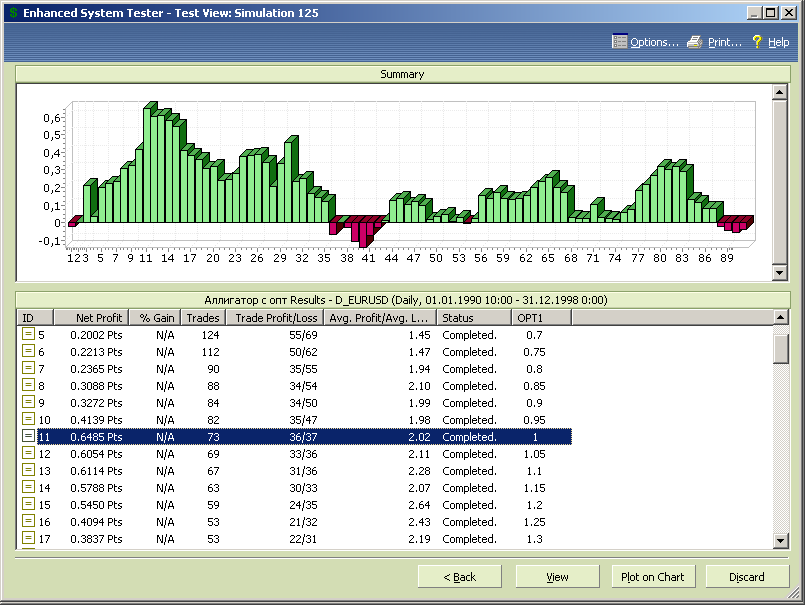
Рис.7.71.
Значение параметра оптимизации, равное единице, соответствует исходным параметрам аллигатора Б.Вильямса. Таким для EURUSD образом тестирование на стартовом сегменте данных показало, что параметры индикатора, заданные Б.Вильямсом, являются оптимальными.
Посмотрим, как поведет себя МТС на всем диапазоне сегментированных исторических данных.
Результаты теста с включением диапазона данных «вне выборки» показали, что значение оптимума по максимуму прибыли практически сохранилось (рис.7.72). Максимум прибыли в окрестности значения параметра оптимизации сместился с 1 на 1.05, и появился дополнительный максимум в окрестности 1.8. Т.е. в целом параметры стратегии сохраняют устойчивость во времени.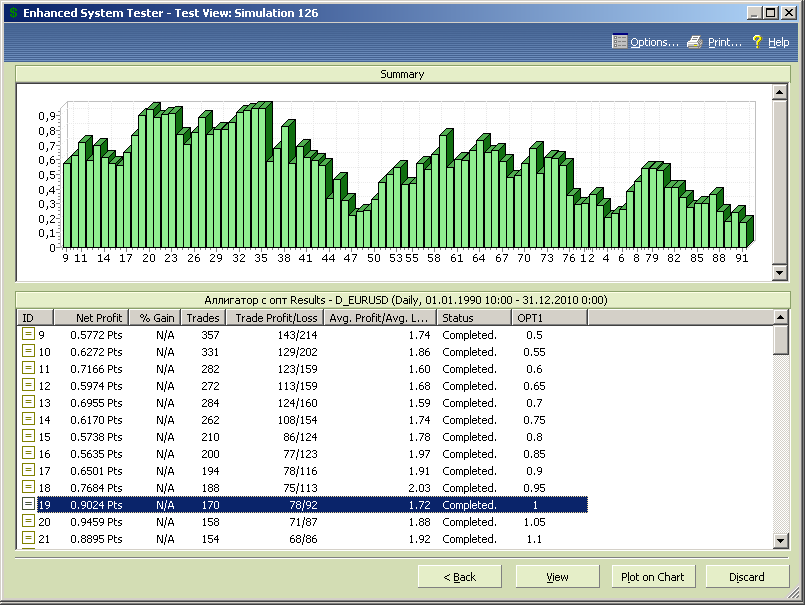
Рис.7.72.
7.11.2. Оптимизация МТС с аллигатором и пробоем локальных экстремумов.
Модифицируем торговые правила п.7.10.8 для проведения оптимизации МТС.
Торговые правила после включения в формулы оптимизационной переменной примут вид:
Buy Order: Cross(C, peak(1,H,0.2))*(C > Mov(Ref((H+L)/2,-3*opt1),9*opt1,E))*(C > Mov(Ref((H+L)/2,-5*opt1),15*opt1,E))*(C > Mov(Ref((H+L)/2,-8*opt1),25*opt1,E))
Sell Order: (C< Mov(Ref((H+L)/2,-5*opt1),15*opt1,E)) OR Cross(Trough(1,L,0.2),C)*(C < Mov(Ref((H+L)/2,-3*opt1),9*opt1,E))*(C < Mov(Ref((H+L)/2,-5*opt1),15*opt1,E))*(C < Mov(Ref((H+L)/2,-8*opt1),25*opt1,E))
Sell Short Order: Cross(Trough(1,L,0.2),C)*(C < Mov(Ref((H+L)/2,-3*opt1),9*opt1,E))*(C < Mov(Ref((H+L)/2,-5*opt1),15*opt1,E))*(C < Mov(Ref((H+L)/2,-8*opt1),25*opt1,E))
Buy to Cover Order: (C> Mov(Ref((H+L)/2,-5*opt1),15*opt1,E)) OR Cross(C, peak(1,H,0.2))*(C > Mov(Ref((H+L)/2,-3*opt1),9*opt1,E))*(C > Mov(Ref((H+L)/2,-5*opt1),15*opt1,E))*(C > Mov(Ref((H+L)/2,-8*opt1),25*opt1,E))
Диапазон оптимизационной переменной зададим от 0.5 до 5 с шагом 0.05.
Проводим первоначальную оптимизацию на стартовом сегменте данных.
Результаты тестирования представлены на графиках рисунка 7.73.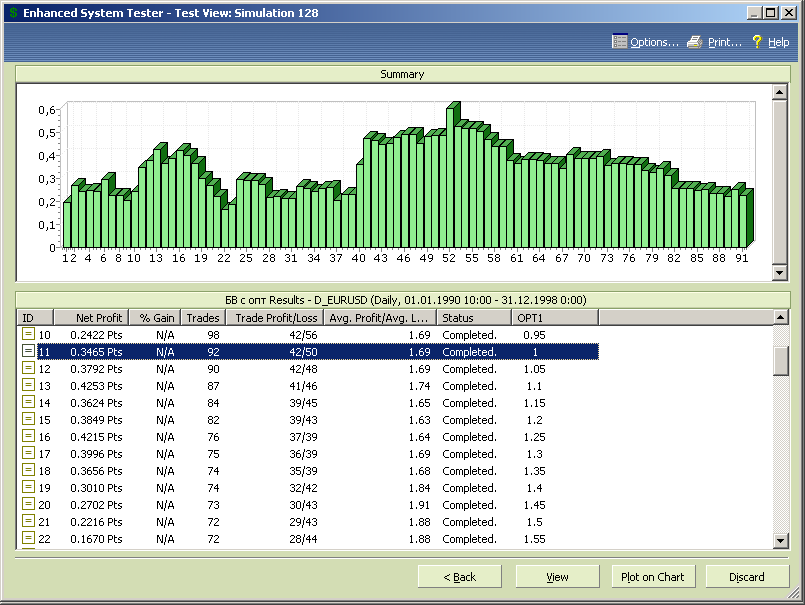
Рис.7.73.
Для этой системы уже пошли отличия.
Во-первых, при значении opt1=1 нет оптимума, даже локального. Локальный максимум соответствует диапазону значений переменной оптимизации от 1.05 до 1.35.
Оптимальное же значение параметра оптимизации по критерию максимума прибыли соответствует opt1=3.05 и обеспечивает прибыль почти в два раза больше, чем при стандартных параметрах аллигатора с opt1=1 (рис.7.74).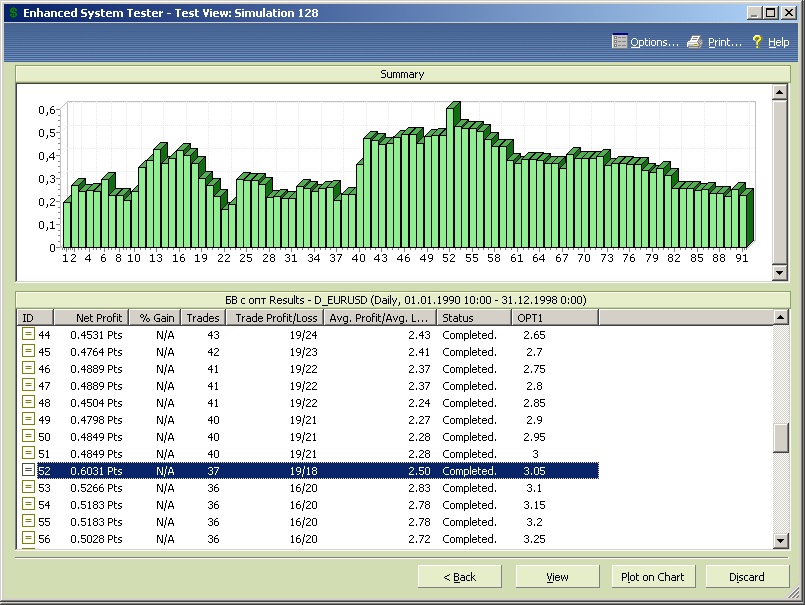
Рис.7.74.
Сравним ход линии эквити для стандартных и оптимальных параметров аллигатора (рис.7.75).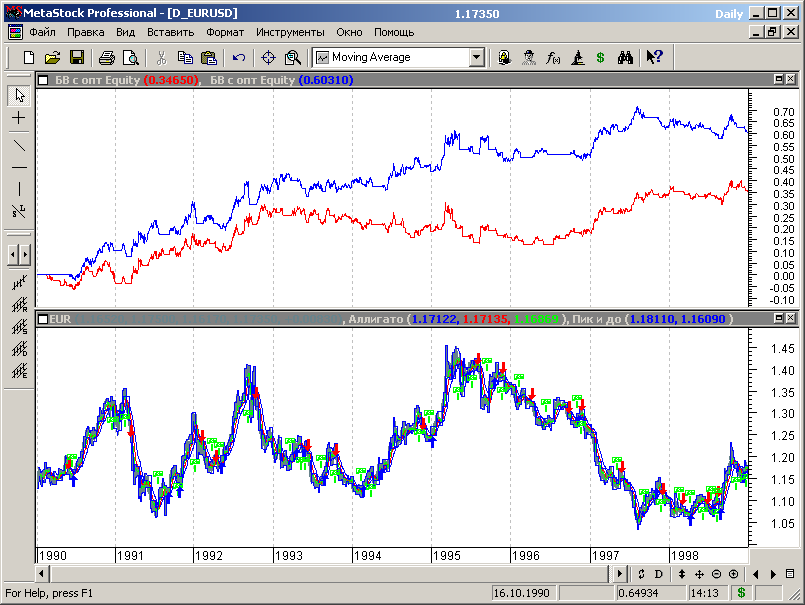
Рис.7.75.
Линия эквити для стандартных параметров аллигатора показана на графике рисунка 7.75 красным цветом, линия эквити для МТС с оптимизацией – синим цветом.
Сравнение представленных зависимостей показывает, что на стартовом сегменте данных система со стандартными параметрами ведет себя значительно хуже оптимальной МТС практически по всем параметрам эквити: прибыль меньше, просадки больше, периоды бесприбыльной и убыточной работы гораздо более продолжительны. Но это на интервале выборки. Посмотрим, сохранится ли указанная картина на данных вне выборки.
Результаты тестирования всем диапазоне сегментированных данных представлены на рисунках 7.76 и 7.77.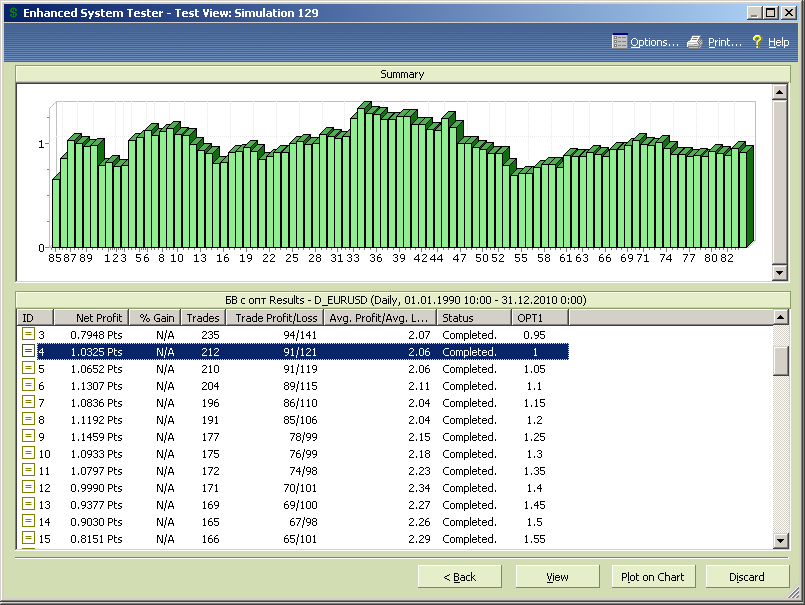
Рис.7.76.
Как и в случае первоначальной оптимизации границы первого оптимума стратегии сохранились для opt1 от 1.05 до 1.35, а МТС со стандартными параметрами аллигатора при opt1=1 находится вблизи нижней границы оптимума.
Оптимальное значение параметра оптимизации по критерию максимума прибыли переместилось на opt1=2.5 (рис.7.77), т.е. динамика рынков ускорилась, однако и значение 3.05 также обеспечивает локальный максимум по полученной прибыли.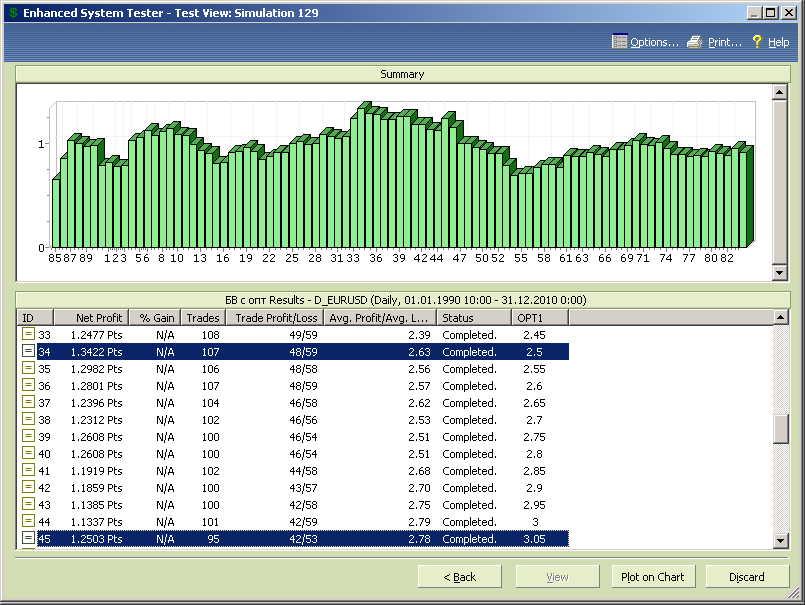
Рис.7.77.
Графики эквити представлены на рисунке 7.78.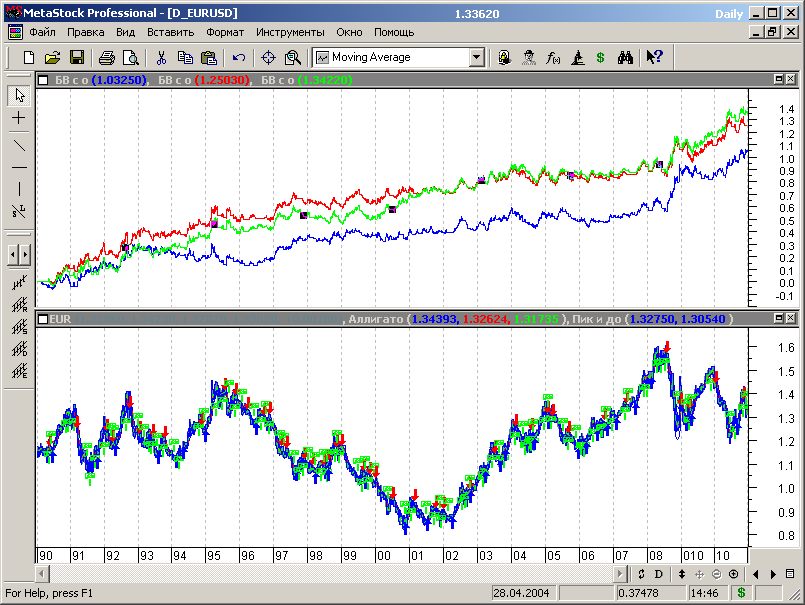
Рис.7.78.
Линия эквити для стандартных параметров аллигатора показана на графике рисунка 7.75 красным цветом, линия эквити для МТС, полученной по результатам первоначальной оптимизации (с opt1=3.05) – синим цветом, линия эквити для системы, оптимизированной на всем диапазоне данных – зеленым цветом.
Положительный эффект от оптимизации налицо.
Прибыль стратегии возросла, выросла и плавность хода эквити по сравнению с МТС, использующей стандартные параметры аллигатора. Торговая стратегия сохраняет устойчивость с течением времени, сохраняя параметры и прибыльную работу на данных «вне выборки». Незначительное отличие хода линий эквити для систем, оптимизированных на стартовом сегменте данных и на всем диапазоне сегментированной истории, позволяет с уверенностью смотреть в будущее при использовании этой торговой стратегии. Постепенное изменение параметров рынка может быть учтено периодической оптимизацией и подстройкой параметров торговой стратегии.
Количественные характеристики теста для трех версий стратегии:
Исходная МТС, со стандартными параметрами аллигатора:
- профит - 10325пп;
- процент прибыльных сделок – 42.9%;
- отношение AW/AL – 2.06;
- профит-фактор – 1.55.
МТС по результатам первоначальной оптимизации:
- профит - 12503пп;
- процент прибыльных сделок –44.2%;
- отношение AW/AL – 2.78;
- профит-фактор – 2.21.
МТС, оптимизированная на всех сегментах данных:
- профит - 13422пп;
- процент прибыльных сделок – 44.9%;
- отношение AW/AL – 2.63;
- профит-фактор – 2.14.
Оба варианта оптимизированных стратегий близки по количественным характеристикам, и превосходят первоначальную торговую стратегию со стандартными параметрами аллигатора.
Таким образом, и в этом случае наши исследования позволили улучшить характеристики первоначальной торговой стратегии, которая была использована в качестве прототипа.
7.12. Резюме.
Мы рассмотрели несколько типовых вариантов построения МТС на основе скользящих средних и научились записывать для таких систем торговые правила в тестере систем Метасток, а также оптимизировать системы с одной и с несколькими оптимизационными переменными.
Рассмотренные нами типовые примеры не исчерпывают все возможное многообразие вариантов применения скользящих средних в качестве элементов торговых систем, но они дают основу для формализации и исследования практически любых торговых стратегий на основе скользящих средних.

Комментариев нет:
Отправить комментарий